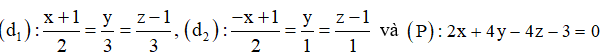Đồng vị phóng xạ \(_{27}^{60}{\rm{Co}}\) phát ra tia γ có khả năng đâm xuyên lớn nên được dùng để tìm khuyết tật trong các chi tiết máy (phương pháp tương tự như dùng tia X để chụp ảnh các bộ phận bên trong cơ thể), để chữa bệnh ung thư, để bảo quản thực phẩm (vì có tác dụng diệt vi khuẩn). Nguồn phóng xạ \(_{27}^{60}{\rm{Co}}\) có chu kì bán rã 5,3 năm nên chỉ cần một lượng thích hợp có thể sử dụng trong thời gian khá dài.
Đâu không phải ứng dụng của đồng vị phóng xạ \(_{27}^{60}{\rm{Co}}\)?
Đồng vị phóng xạ \(_{27}^{60}{\rm{Co}}\) phát ra tia γ có khả năng đâm xuyên lớn nên được dùng để tìm khuyết tật trong các chi tiết máy (phương pháp tương tự như dùng tia X để chụp ảnh các bộ phận bên trong cơ thể), để chữa bệnh ung thư, để bảo quản thực phẩm (vì có tác dụng diệt vi khuẩn). Nguồn phóng xạ \(_{27}^{60}{\rm{Co}}\) có chu kì bán rã 5,3 năm nên chỉ cần một lượng thích hợp có thể sử dụng trong thời gian khá dài.
Đâu không phải ứng dụng của đồng vị phóng xạ \(_{27}^{60}{\rm{Co}}\)?
Quảng cáo
Trả lời:
Đáp án đúng là D
Ứng dụng của tia gamma:
- Tìm khuyết tật trong vật đúc;
- Xạ trị trong chữa ung thư;
- Bảo quản thực phẩm.
Câu hỏi cùng đoạn
Câu 2:
Đồng vị \(_{27}^{60}{\rm{Co}}\) chất phóng xạ β- tạo thành hạt nhân con là
Đáp án đúng là C
\(_{27}^{60}{\rm{Co}} \to \,_{ - 1}^0\beta + _{28}^{60}{\rm{X}}\) nên X là \(_{28}^{60}{\rm{Ni}}\).
Câu 3:
Ban đầu có một lượng phóng xạ \(_{27}^{60}{\rm{Co}}\) nguyên chất. Sau 30 năm lượng chất Co đã bị phân rã bao nhiêu phần trăm?
Ban đầu có một lượng phóng xạ \(_{27}^{60}{\rm{Co}}\) nguyên chất. Sau 30 năm lượng chất Co đã bị phân rã bao nhiêu phần trăm?
Đáp án đúng là A
Chu kì bán rã \(T = 5,3\) năm.
\(\frac{{{N_0} - N}}{{{N_0}}} = 1 - {.2^{\frac{{ - t}}{T}}} = 1 - {2^{ - \frac{{30}}{{5,3}}}} = 0,9802\). Vậy lượng chất Co đã bị phân rã là 98,02%.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Nếu gửi ở ngân hàng có lãi suất \(6\% /\)năm thì sau 2 năm số tiền cả vốn lẫn lãi thu được là: \(50{\left( {1 + \frac{6}{{100}}} \right)^2} = 56,18\) (triệu đồng).
Đáp án cần nhập là: 56,18.
Câu 2
Lời giải
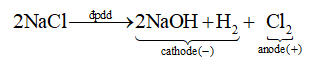
Chọn A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.