1) Cho \(\Delta ABC\) trung tuyến \(AD.\) Vẽ tia phân giác của \[\widehat {ADB}\] cắt \(AB\) tại \(M,\) tia phân giác của \[\widehat {ADC}\] cắt \(AC\) tại \(N.\) Chứng minh rằng:
a) \[\frac{{MB}}{{MA}} = \frac{{BD}}{{AD}}.\] b) \(MN\,{\rm{//}}\,BC.\)
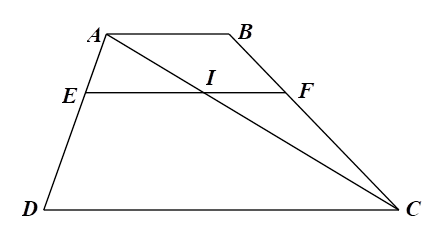
2) Cho tam giác \(ABC\) có \(AB < AC.\) Tia phân giác \(\widehat {BAC}\) cắt cạnh \(BC\) tại điểm \(D.\) Gọi \(M\) là trung điểm của cạnh \(BC.\) Qua điểm \(M\) kẻ đường thẳng song song với đường thẳng \(AD\) cắt các đường thẳng \(AC,\,\,AB\) lần lượt tại \(E\) và \(K.\) Chứng minh rằng:
a) Tam giác \(AEK\) cân. b) \(BK = EC.\)
1) Cho \(\Delta ABC\) trung tuyến \(AD.\) Vẽ tia phân giác của \[\widehat {ADB}\] cắt \(AB\) tại \(M,\) tia phân giác của \[\widehat {ADC}\] cắt \(AC\) tại \(N.\) Chứng minh rằng:
a) \[\frac{{MB}}{{MA}} = \frac{{BD}}{{AD}}.\] b) \(MN\,{\rm{//}}\,BC.\)
2) Cho tam giác \(ABC\) có \(AB < AC.\) Tia phân giác \(\widehat {BAC}\) cắt cạnh \(BC\) tại điểm \(D.\) Gọi \(M\) là trung điểm của cạnh \(BC.\) Qua điểm \(M\) kẻ đường thẳng song song với đường thẳng \(AD\) cắt các đường thẳng \(AC,\,\,AB\) lần lượt tại \(E\) và \(K.\) Chứng minh rằng:
a) Tam giác \(AEK\) cân. b) \(BK = EC.\)
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
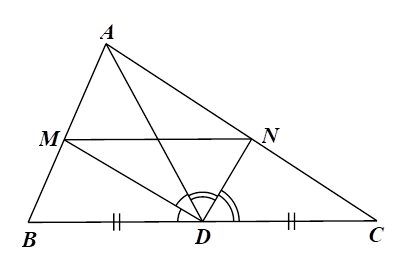
a) Xét \(\Delta ABD\) có \(DM\) là đường phân giác của \[\widehat {ADB}\] nên \[\frac{{DA}}{{DB}} = \frac{{MA}}{{MB}}\] (tính chất đường phân giác trong tam giác).
b) Xét \(\Delta ACD\) có \(DN\) là đường phân giác của \[\widehat {ADC}\] nên \[\frac{{DA}}{{DC}} = \frac{{NA}}{{NC}}\] (tính chất đường phân giác trong tam giác).Mà \[\frac{{DA}}{{DB}} = \frac{{MA}}{{MB}}\] (câu a) và \[DB = DC\] nên \[\frac{{MB}}{{MA}} = \frac{{NC}}{{NA}}.\]
Xét \(\Delta ABC\) có: \[\frac{{MB}}{{MA}} = \frac{{NC}}{{NA}}\] (câu b) nên \[MN\,{\rm{//}}\,BC\](định lí Thalès đảo).
Tam giác \(AEK\) có \(\widehat {AKE} = \widehat {AEK}\) nên là tam giác cân tại \(A.\)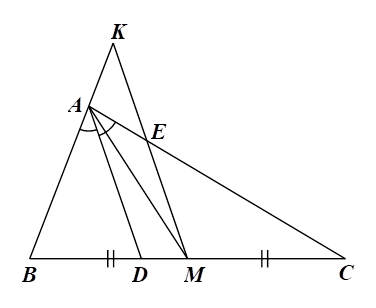
a) Vì \(AD\,{\rm{//}}\,KM\) nên \(\widehat {BAD} = \widehat {BKM}\) (đồng vị).
Vì \(AD\,{\rm{//}}\,EM\) nên \(\widehat {CAD} = \widehat {CEM}\) (đồng vị).
Mà \(AD\) là tia phân giác của \(\widehat {BAC}\) nên \(\widehat {BAD} = \widehat {CAD}.\)
Do đó \(\widehat {BKM} = \widehat {CEM},\) lại có \(\widehat {CEM} = \widehat {AEK}\) nên \(\widehat {BKM} = \widehat {AEK}\) hay \(\widehat {AKE} = \widehat {AEK}.\)b) Xét \(\Delta ACD\) có \(EM\,{\rm{//}}\,AD,\) theo định lí Thalès ta có \(\frac{{AE}}{{EC}} = \frac{{DM}}{{MC}}.\)
Mà \(\Delta AEK\) cân tại \(A\) nên \(AK = AE.\)
Lại có điểm \(M\) là trung điểm của \(BC\) nên \(MB = MC.\)
Do đó \(\frac{{AK}}{{EC}} = \frac{{DM}}{{MB}}.\)
Xét \(\Delta BMK\) có \(AD\,{\rm{//}}\,KM,\) theo định lí Thalès ta có \(\frac{{DM}}{{BM}} = \frac{{AK}}{{BK}}.\)
Mà \(\frac{{AK}}{{EC}} = \frac{{DM}}{{MB}}\) nên \(\frac{{AK}}{{EC}} = \frac{{AK}}{{BK}},\) do đó \(EC = BK.\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
a) Tổ Cường có 3 bạn nam và 1 bạn nữ tham gia vào câu lạc bộ thể thao, nên xác suất của biến cố “Bạn được chọn có tham gia câu lạc bộ thể thao” là \(\frac{{3 + 1}}{{13}} = \frac{4}{{13}}.\)
b) Tổ Cường có 1 bạn nữ tham gia vào câu lạc bộ thể thao, nên xác suất của biến cố “Bạn được chọn là bạn nữ tham gia vào câu lạc bộ thể thao” là \(\frac{1}{{13}}.\)
c) Tổ Cường có 8 bạn nam, trong đó có 3 bạn nam tham gia vào câu lạc bộ thể thao. Khi đó có \(8 - 3 = 5\) bạn nam không tham gia câu lạc bộ thể thao.
Vậy xác suất của biến cố “Bạn được chọn là bạn nam không tham gia câu lạc bộ thể thao” là \(\frac{5}{{13}}.\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
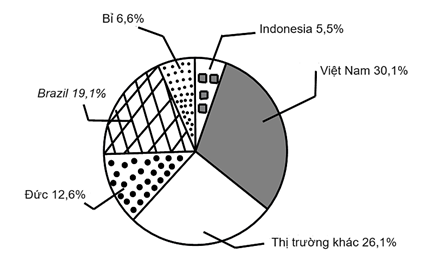
a) Trong 7 tháng đầu năm 2022 thị trường Việt Nam cung cấp cà phê cho Tây Ban Nha là nhiều nhất \(\left( {30,1\% } \right)\) và thị trường Indonesia cung cấp cà phê cho Tây Ban Nha là ít nhất \(\left( {5,5\% } \right).\)
b) i) Lượng cà phê thị trường Đức cung cấp cho Tây Ban Nha trong 7 tháng đầu năm 2022 là: \[222{\rm{ }}956 \cdot 12,6\% = 28\,\,092,456\] (tấn).
Tương tự, ta hoàn thành được bảng thống kê như sau:
|
Thị trường |
Đức |
Brazil |
Bỉ |
Indonesia |
Việt Nam |
Khác |
|
Lượng cà phê (tấn) |
\[28\,\,092,456\] |
\[42\,\,584,596\] |
\(14\,\,715,096\) |
\(12\,\,262,58\) |
\[67\,\,109,756\] |
\(58\,\,191,516\) |
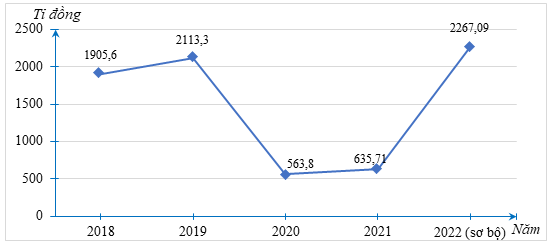
ii) Ta có thể vẽ biểu đồ cột hoặc biểu đồ đoạn thẳng để biểu diễn dữ liệu cho bảng thống kê trên như sau:
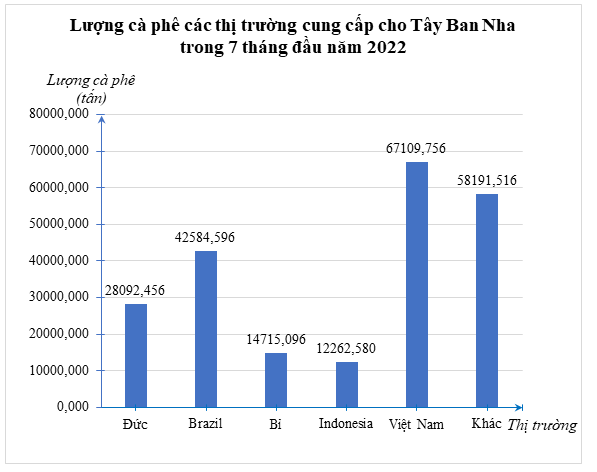
c) Lượng cà phê mà thị trường Việt Nam cung cấp cho Tây Ban Nha gấp \(\frac{{67\,\,109,756}}{{28\,\,092,456}} \approx 2,4\) lần thị trường Đức.
d) Thị trường Indonesia \(\left( {5,5\% } \right)\) và Bỉ \(\left( {6,6\% } \right)\) là hai thị trường cung cấp lượng cà phê ít nhất cho Tây Ban Nha trong 7 tháng đầu năm 2022.
Việt Nam cung cấp cà phê cho Tây Ban Nha nhiều hơn so với thị trường Indonesia là \(30,1\% - 5,5\% = 24,6\% .\)
Vậy bài báo nêu thông tin chính xác.
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập