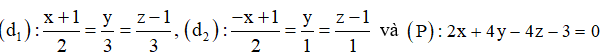Cho hai chất hữu cơ mạch hở E, F có cùng công thức đơn giản nhất là \[{C_3}{H_4}{O_2}.\] Các chất E, F, X, Z tham gia phản ứng theo đúng tỉ lệ mol như sơ đồ dưới đây:
(1) E + NaOH ® X + Y (2) F + NaOH ® Z + T
(3) X + HCl ® J + NaCl (4) Z + HCl ® G + NaCl
Biết: X, Y, Z, T, J, G là các chất hữu cơ, trong đó T đa chức; \[{M_T} > {\rm{ }}88\] và \[{M_E} < {\rm{ }}{M_F} < {\rm{ }}146.\] Cho các phát biểu sau:
(a) Chất J có nhiều trong nọc độc con kiến.
(b) Từ Y có thể điều chế trực tiếp được acetic acid.
(c) Ở nhiệt độ thường, T tác dụng với \[Cu{\left( {OH} \right)_2}\] tạo dung dịch xanh lam.
(d) E và F đều tạo kết tủa khi cho tác dụng với \[AgN{O_3}\] trong dung dịch \[N{H_3}.\]
(e) Nung nóng chất rắn Z với hỗn hợp vôi tôi xút thu được khí ethylene.
Số phát biểu đúng là
Cho hai chất hữu cơ mạch hở E, F có cùng công thức đơn giản nhất là \[{C_3}{H_4}{O_2}.\] Các chất E, F, X, Z tham gia phản ứng theo đúng tỉ lệ mol như sơ đồ dưới đây:
(1) E + NaOH ® X + Y (2) F + NaOH ® Z + T
(3) X + HCl ® J + NaCl (4) Z + HCl ® G + NaCl
Biết: X, Y, Z, T, J, G là các chất hữu cơ, trong đó T đa chức; \[{M_T} > {\rm{ }}88\] và \[{M_E} < {\rm{ }}{M_F} < {\rm{ }}146.\] Cho các phát biểu sau:
(a) Chất J có nhiều trong nọc độc con kiến.
(b) Từ Y có thể điều chế trực tiếp được acetic acid.
(c) Ở nhiệt độ thường, T tác dụng với \[Cu{\left( {OH} \right)_2}\] tạo dung dịch xanh lam.
(d) E và F đều tạo kết tủa khi cho tác dụng với \[AgN{O_3}\] trong dung dịch \[N{H_3}.\]
(e) Nung nóng chất rắn Z với hỗn hợp vôi tôi xút thu được khí ethylene.
Số phát biểu đúng là
Quảng cáo
Trả lời:
\[{M_E}\; < {M_F}\; < 146\] và E, F có cùng công thức đơn giản nhất là \[{C_3}{H_4}{O_2}\]Þ E là \[{C_3}{H_4}{O_2}\] và F là \[{C_6}{H_8}{O_4}.\]
E + NaOH tạo 2 sản phẩm hữu cơ nên E là \[HCOOCH = C{H_2}.\]
Þ X là HCOONa; Y là \[C{H_3}CHO\] và J là HCOOH.
F tác dụng với NaOH theo tỉ lệ mol 1 : 1 và tạo 2 sản phẩm hữu cơ nên F chứa 1 chức ester.
T là chất hữu cơ đa chức nên F là \[CH \equiv C - COO - C{H_2} - CHOH - C{H_2}OH.\]
Z là CH≡C−COONa và T là \[{C_3}{H_5}{\left( {OH} \right)_3}.\]
Vậy ta có:
(a) Đúng, J (HCOOH) có nhiều trong nọc độc con kiến.
(b) Đúng, CH3CHO + O2 CH3COOH
(c) Đúng, T (\[{C_3}{H_5}{\left( {OH} \right)_3}\]) có 3 nhóm −OH liền kề nên tác dụng với \[Cu{\left( {OH} \right)_2}\] tạo dung dịch xanh lam.
(d) Đúng, E tạo kết tủa Ag và F tạo kết tủa \[CAg \equiv C - COO - C{H_2} - CHOH - C{H_2}OH.\]
(e) Sai, Z + NaOH → \[{C_2}{H_2}\; + {\rm{ }}N{a_2}C{O_3}.\]
Chọn B.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Nếu gửi ở ngân hàng có lãi suất \(6\% /\)năm thì sau 2 năm số tiền cả vốn lẫn lãi thu được là: \(50{\left( {1 + \frac{6}{{100}}} \right)^2} = 56,18\) (triệu đồng).
Đáp án cần nhập là: 56,18.
Câu 2
Lời giải
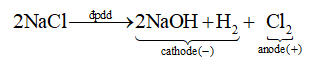
Chọn A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.