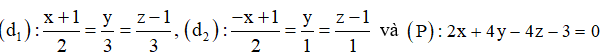Phân tích nguyên tố hợp chất hữu cơ đơn chức E cho kết quả phần trăm khối lượng C, H và O lần lượt là 54,55%; 9,09% và 36,36%. Phổ hồng ngoại IR của E có dạng như sau:
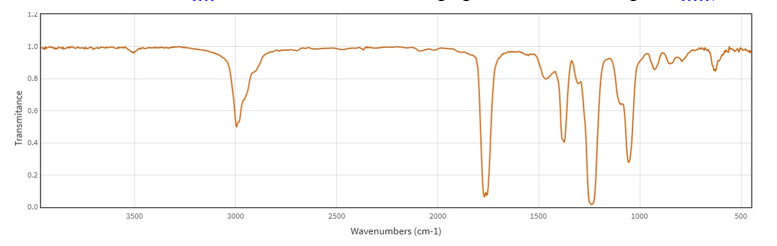
Thủy phân hoàn toàn E trong dung dịch NaOH, thu được muối của carboxylic acid X và chất Y. Đốt cháy Y với cùng số mol E thì số mol CO2 của Y bằng một nửa của E.
Cho các phát biểu sau:
(a). Nhiệt độ sôi của E, X, Y được xếp theo thứ tự tăng dần là Y, E, X.
(b). Từ X có thể điều chế trực tiếp ra Y.
(c). Y có vai trò chính trong nước rửa tay sát khuẩn thông thường.
(d). Có thể tách E ra khỏi hỗn hợp E, X, Y bằng phương pháp chiết.
Số phát biểu đúng là (nhập đáp án vào ô trống)?
Đáp án __
Quảng cáo
Trả lời:
Đặt công thức cấu tạo của X có dạng: CxHyOz. Ta có:
\(x:y:z = \frac{{54,55}}{{12}}:\frac{{9,09}}{1}:\frac{{36,36}}{{16}} = 4,55:9,09:2,27 = 2:4:1\)
Từ phổ hồng ngoại của E xác định được E là ester.
Lại có E đơn chức nên công thức phân tử của E là: \({C_4}{H_8}{O_2}.\)
Đốt cháy Y (là alcohol) với cùng số mol E thì số mol CO2 của Y bằng một nửa của E. Vậy công thức cấu tạo của E là: CH3COOC2H5; Y là C2H5OH và X là: CH3COONa.
Phát biểu (a) sai, vì: Nhiệt độ sôi của E, X, Y được xếp theo thứ tự tăng dần là E, Y, X.
Phát biểu (b) sai, vì: Từ CH3COONa không thể điều chế trực tiếp ra C2H5OH.
Phát biểu (c) đúng.
Phát biểu (đ) đúng.
Đáp án: 2.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Nếu gửi ở ngân hàng có lãi suất \(6\% /\)năm thì sau 2 năm số tiền cả vốn lẫn lãi thu được là: \(50{\left( {1 + \frac{6}{{100}}} \right)^2} = 56,18\) (triệu đồng).
Đáp án cần nhập là: 56,18.
Câu 2
Lời giải
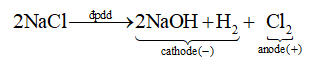
Chọn A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.