Cho tam giác \[MNP,\] trên \[MN\] lấy hai điểm \[D,{\rm{ }}E\] sao cho \[MD = DE = EN.\] Gọi \[I\] là trung điểm \[NP,{\rm{ }}PD\] cắt \[MI\] tại \[H.\] Khẳng định nào sau đây là đúng?
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: B
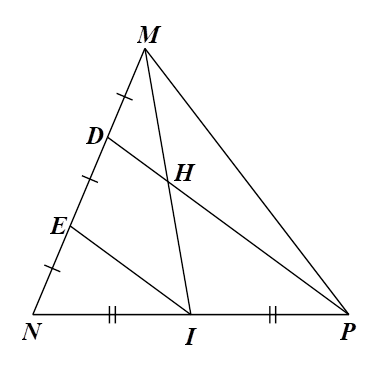
Trong \[\Delta NDP\] có \[I,\,\,E\] lần lượt là trung điểm của \[NP,\] \[DN\] (do \[DE = EN).\]
Do đó \[EI\] là đường trung bình của \(\Delta NDP.\)
Suy ra \[EI\,{\rm{//}}\,PD\] và \(EI = \frac{1}{2}PD\) (tính chất đường trung bình của tam giác) (1).
Trong \(\Delta MEI\) có \[D\] là trung điểm \[ME\] (do \[MD = DE),\] \[DH\,{\rm{//}}\,EI{\rm{ }}\left( {H \in DP} \right).\]
Suy ra \[H\] là trung điểm của \[MI.\]
Nên \[HD\] là đường trung bình của \(\Delta MEI.\)
Suy ra \(HD = \frac{1}{2}EI\) (tính chất đường trung bình của tam giác) (2).
Từ (1) và (2) suy ra \(HD = \frac{1}{2}EI = \frac{1}{2} \cdot \frac{1}{2}PD = \frac{1}{4}PD.\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
a) Để hàm số đã cho là hàm số bậc nhất thì \(3 - m \ne 0,\) hay \(m \ne 3.\)
b) Để đường thẳng \[y = \left( {3--m} \right)x + 3m + 2\] đi qua điểm \[\left( {1;3} \right)\] thì \(x = 1\) và \(y = 3\) thỏa mãn hàm số trên.
Do đó ta có: \[3 = \left( {3--m} \right) \cdot 1 + 3m + 2\]
\[3 = 3--m + 3m + 2\]
\[2m = - 2\]
\(m = - 1.\)
Vậy \(m = - 1\) thỏa mãn yêu cầu đề bài.
c) Để đường thẳng \[y = \left( {3--m} \right)x + 3m + 2\] cắt đường thẳng \[y = x--1\] thì \(3 - m \ne 1,\) do đó \(m \ne 2.\)
Gọi \(A\left( {{x_A};{y_A}} \right)\) là giao điểm của hai đường thẳng.
Để hai đường thẳng trên cắt nhau tại điểm \(A\left( {{x_A};{y_A}} \right)\) nằm trên trục tung thì \({x_A} = 0.\)
Thay \({x_A} = 0\) vào hàm số \[y = x--1\] ta được \({y_A} = 0 - 1 = - 1.\)
Thay \({x_A} = 0\) và \({y_A} = - 1\) vào hàm số \[y = \left( {3--m} \right)x + 3m + 2\] ta được:
\[ - 1 = \left( {3--m} \right) \cdot 0 + 3m + 2\]
\[ - 1 = 3m + 2\]
\[m = - 1\] (thỏa mãn \(m \ne 2).\)
Vậy \(m = - 1\) thỏa mãn yêu cầu đề bài.
Câu 2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
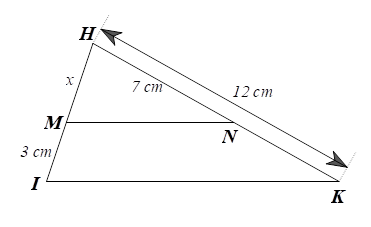
Xét \(\Delta HIK\) có \(MN\,{\rm{//}}\,IK,\) theo định lí Thalès ta có: \(\frac{{MH}}{{MI}} = \frac{{NH}}{{NK}}.\)
Suy ra \(\frac{x}{3} = \frac{7}{{12 - 7}},\) do đó \(x = \frac{{3 \cdot 7}}{5} = 4,2{\rm{\;cm}}{\rm{.}}\)
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập