Cho tam giác \(ABC\) cân tại \(A\) có \(\widehat A = 2\alpha \). Số đo góc \(\widehat B\) theo \(\alpha \) là
Quảng cáo
Trả lời:
Đáp án đúng là: C
Do tam giác \(ABC\) cân tại \(A\) có \(\widehat A = 2\alpha \) nên \(\widehat B = \widehat C\).
Áp dụng định lí tổng ba góc trong một tam giác, ta có:
\(\widehat A + \widehat B + \widehat C = 180^\circ \) suy ra \(2\widehat B = 180^\circ - \widehat A = 180^\circ - 2\alpha \).
Do đó, \(\widehat B = \frac{{180^\circ - 2\alpha }}{2} = 90^\circ - \alpha .\)
Vậy chọn đáp án C.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Toán - Văn - Anh, Toán - Anh - KHTN lớp 6 (chương trình mới) ( 126.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
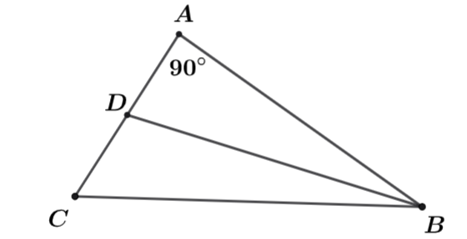
a) \(\widehat {ABC} = 40^\circ \).
b) \(\widehat {ABD} = \widehat {DBC} = 20^\circ .\)
c) \(\widehat {ADB} < \widehat {ACB}\).
Lời giải
a) Đúng.
Xét \(\Delta ABC\) có: \(\widehat A + \widehat B + \widehat C = 180^\circ \) (tổng ba góc trong tam giác)
Suy ra \(\widehat B = 180^\circ - \left( {\widehat A + \widehat C} \right) = 180^\circ - \left( {90^\circ + 50^\circ } \right) = 40^\circ \).
b) Đúng.
Vì \(BD\) là phân giác của \(\widehat B\) nên ta có: \(\widehat {ABD} = \widehat {DBC} = \frac{1}{2}\widehat {ABC} = 20^\circ .\)
c) Sai.
Xét tam giác \(ADB,\) có: \(\widehat {ADB} + \widehat {DAB} + \widehat {ABD} = 180^\circ \) (tổng ba góc trong tam giác)
Suy ra \(\widehat {ADB} = 180^\circ - \left( {\widehat {DAB} + \widehat {ABD}} \right) = 180^\circ - \left( {90^\circ + 20^\circ } \right) = 70^\circ > 50^\circ \).
Do đó, \(\widehat {ADB} > \widehat {ACB}\).
d) Đúng.
Vì \(\widehat {ADB},\widehat {\,CDB}\) là hai góc kề bù, nên \(\widehat {ADB} + \widehat {CDB} = 180^\circ \)
Suy ra \(\widehat {\,CDB} = 180 - \widehat {ADB} = 180^\circ - 70^\circ = 110^\circ \).
Do đó, \(\widehat {\,CDB}\) là góc tù.
Câu 2
Lời giải
Đáp án đúng là: B
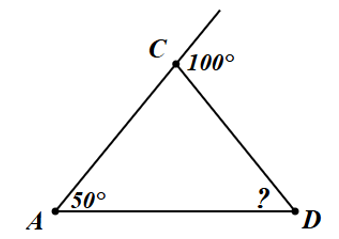
Ta có: \(\widehat {ACD} = 180^\circ - 100^\circ = 80^\circ \).
Xét tam giác \(ACD\), có: \(\widehat {CAD} + \widehat {ADC} + \widehat {DCA} = 180^\circ \) (tổng ba góc trong tam giác)
Suy ra \(\widehat {ADC} = 180^\circ - 50^\circ - 80^\circ = 50^\circ \).
Câu 3
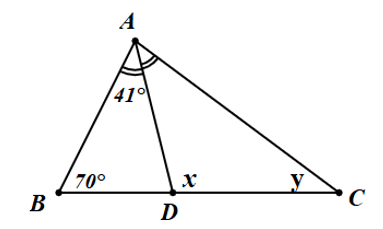
a) \(\widehat {BDA} = 79^\circ .\)
b) \(x = 111^\circ .\)
c) \(\widehat {BAC} = 81^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
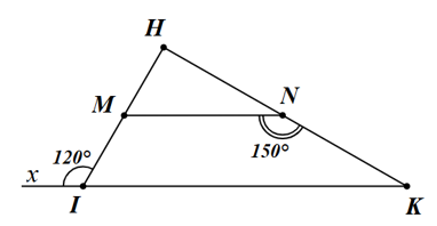
a) \(\widehat {HIK} = 60^\circ .\)
b) \(\widehat {HMN} = 60^\circ \).
c) \(2\widehat {HNM} = \widehat {HMN}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
a) \(\widehat {BAC} = 60^\circ \).
b) \(\widehat {IBC} = 40^\circ .\)
c) \(\widehat {ICB} = 20^\circ .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.