Giả sử rằng lượng cung \[S\] và lượng cầu \[D\] về áo phông tại một buổi biểu diễn được cho bởi các hàm số sau:
\[S\left( p \right) = --600 + 10p;{\rm{ }}\,\,\,D\left( p \right) = 1{\rm{ }}200--20p,\]
trong đó \[p\] (nghìn đồng) là giá của một chiếc áo phông.
a) Tìm mức giá cân bằng (tức là mức giá mà lượng cung bằng lượng cầu) của áo phông tại buổi biểu diễn này.
b) Vẽ đồ thị của hai hàm số \[S\left( p \right)\] và \[D\left( p \right)\] trên cùng một hệ trục tọa độ.
c) Từ đồ thị vẽ được ở câu b, xác định mức giá của áo phông mà lượng cung lớn hơn lượng cầu. Khi đó, điều gì sẽ xảy ra?
Giả sử rằng lượng cung \[S\] và lượng cầu \[D\] về áo phông tại một buổi biểu diễn được cho bởi các hàm số sau:
\[S\left( p \right) = --600 + 10p;{\rm{ }}\,\,\,D\left( p \right) = 1{\rm{ }}200--20p,\]
trong đó \[p\] (nghìn đồng) là giá của một chiếc áo phông.
a) Tìm mức giá cân bằng (tức là mức giá mà lượng cung bằng lượng cầu) của áo phông tại buổi biểu diễn này.
b) Vẽ đồ thị của hai hàm số \[S\left( p \right)\] và \[D\left( p \right)\] trên cùng một hệ trục tọa độ.
c) Từ đồ thị vẽ được ở câu b, xác định mức giá của áo phông mà lượng cung lớn hơn lượng cầu. Khi đó, điều gì sẽ xảy ra?
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
a) Mức giá khi lượng cung bằng lượng cầu là giá trị \[{x_0}\] thỏa mãn:
\[--600 + 10{x_0} = 1{\rm{ }}200--20{x_0}\]
\[30{x_0} = 1{\rm{ }}800\]
\[{x_0} = 60\]
Vậy mức giá cân bằng là 60 nghìn đồng.
b) Đồ thị hàm số \[S\left( p \right)\] đi qua hai điểm \[\left( {0;--600} \right)\] và \[\left( {60;{\rm{ }}0} \right).\]
Đồ thị hàm số \[D\left( p \right)\] đi qua hai điểm \[\left( {0;{\rm{ }}1{\rm{ }}200} \right)\] và \[\left( {60;{\rm{ }}0} \right).\]
Đồ thị của hai hàm số được vẽ trong hình dưới:
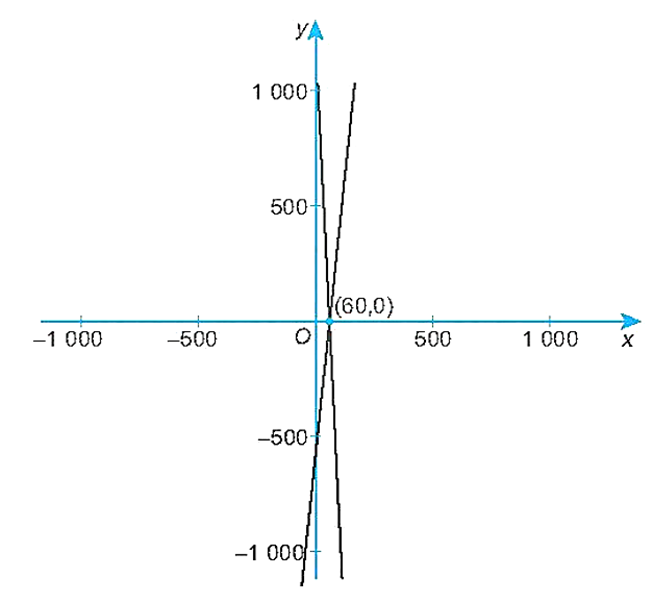
c) Từ đồ thị trên, ta thấy khi giá của mỗi chiếc áo lớn hơn 60 nghìn đồng thì lượng cung lớn hơn lượng cầu. Khi đó sẽ có một lượng áo phông bị tồn kho (do không bán được).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
1)
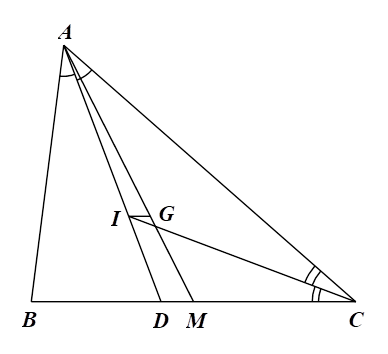
a) Gọi \(AD\) là đường phân giác góc \(BAC\) \(\left( {D \in BC} \right).\)
Xét \(\Delta ABC\) có \(AD\) là đường phân giác của \(\widehat {BAC}\) nên \[\frac{{AB}}{{AC}} = \frac{{DB}}{{DC}},\] hay \[\frac{{DC}}{{AC}} = \frac{{DB}}{{AB}}.\]
Theo tính chất dãy tỉ số bằng nhau ta có:
\[\frac{{DC}}{{AC}} = \frac{{DB}}{{AB}} = \frac{{DC + DB}}{{AC + AB}} = \frac{{BC}}{{AC + AB}} = \frac{{15}}{{18 + 12}} = \frac{1}{2}.\]Suy ra \(CD = \frac{1}{2}AC = \frac{1}{2} \cdot 18 = 9{\rm{\;cm}}\) và \(BD = \frac{1}{2}AB = \frac{1}{2} \cdot 12 = 6{\rm{\;cm}}.\)
b) Xét \(\Delta ACD,\) có \(CI\) là đường phân giác của \(\widehat {ACD}\) nên \(\frac{{AI}}{{DI}} = \frac{{AC}}{{CD}} = \frac{{18}}{9} = 2.\)
Mặt khác, do \(G\) là trọng tâm của \(\Delta ABC\) nên \(\frac{{AG}}{{GM}} = 2.\)
Do đó \(\frac{{AI}}{{ID}} = \frac{{AG}}{{GM}} = 2,\) theo định lí Thalès đảo ta có \(IG\,{\rm{//}}\,BC.\)
b) Gọi \(M\) là trung điểm của \(BC.\) Khi đó \[MB = MC = \frac{1}{2}BC = \frac{1}{2} \cdot 15 = 7,5{\rm{\;cm}}.\]
Suy ra \(DM = BM - BD = 7,5 - 6 = 1,5{\rm{\;cm}}.\)
Xét \(\Delta ADM\) có \(IG\,{\rm{//}}\,BC,\) theo hệ quả định lí Thalès ta có \(\frac{{IG}}{{DM}} = \frac{{AG}}{{AM}} = \frac{2}{3}.\)
Suy ra \(IG = \frac{2}{3}DM = \frac{2}{3} \cdot 1,5 = 1{\rm{\;cm}}.\)
2)
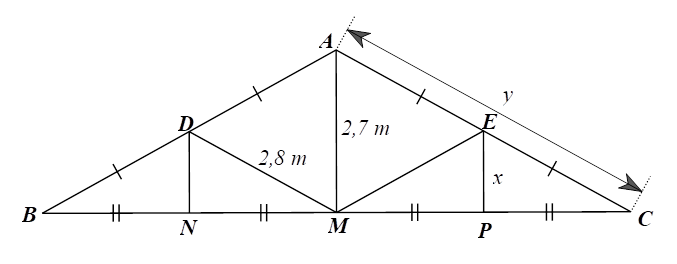
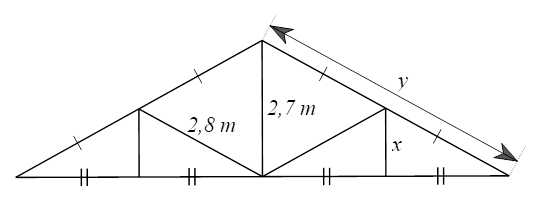
Đặt các điểm \[A,{\rm{ }}B,{\rm{ }}C,{\rm{ }}D,{\rm{ }}E,{\rm{ }}M,{\rm{ }}N,{\rm{ }}P\] như hình vẽ trên.
⦁ Xét \(\Delta AMC\) có \(E,\,\,P\) lần lượt là trung điểm của \(AC,\,\,MC\) (do \(EA = EC,PM = PC)\) nên \(EP\) là đường trung bình của \(\Delta AMC.\)
Do đó \(EP = \frac{1}{2}AM = \frac{1}{2} \cdot 2,7 = 1,35{\rm{\;}}\left( {\rm{m}} \right)\) (tính chất đường trung bình của tam giác).
Hay \(x = 1,35{\rm{\;}}\left( {\rm{m}} \right){\rm{.}}\)
⦁ Ta có \(MB = MN + NB\) và \(MC = MP + PC\)
Mà \(MN = NB = MP = PC\) nên \(MB = MC.\)
Xét \(\Delta ABC\) có \(D,\,\,M\) lần lượt là trung điểm của \(AB,\,\,BC\) (do \(DB = DA,MB = MC)\) nên \(DM\) là đường trung bình của \(\Delta ABC.\)
Do đó \[DM = \frac{1}{2}AC\] (tính chất đường trung bình của tam giác).
Suy ra \(AC = 2DM = 2 \cdot 2,8 = 5,6{\rm{\;}}\left( {\rm{m}} \right).\) Hay \[y = 5,6{\rm{\;}}\left( {\rm{m}} \right).\]
Vậy độ dài của cây chống đứng bên và độ dài của của cánh kèo lần lượt là \(x = 1,35{\rm{\;}}\left( {\rm{m}} \right);\) \(y = 5,6{\rm{\;}}\left( {\rm{m}} \right).\)
Câu 2
A. \(4{\rm{\;cm}}.\)
B. \(4,5{\rm{\;cm}}.\)
C. \(3,5{\rm{\;cm}}.\)
D. \(14{\rm{\;cm}}.\)
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
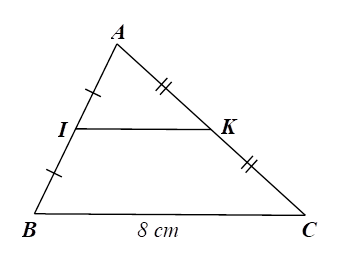
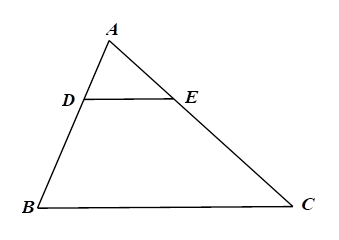
Xét \(\Delta ABC\) có \(I,\,\,K\) lần lượt là trung điểm của \(AB\) và \(AC\) nên \(IK\) là đường trung bình của tam giác, do đó \(\frac{{IK}}{{BC}} = \frac{1}{2},\) suy ra \(IK = \frac{{BC}}{2} = \frac{8}{2} = 4{\rm{\;cm}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\frac{{AB}}{{BD}} = \frac{{AC}}{{BC}}.\)
B. \(\frac{{AD}}{{AC}} = \frac{{BD}}{{DC}}.\)
C. \[\frac{{DB}}{{AB}} = \frac{{DC}}{{AC}}.\]
D. \(\frac{{DB}}{{DC}} = \frac{{BC}}{{AC}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(\left( {0; - 2} \right).\)
B. \(\left( {1;3} \right).\)
C. \(\left( { - 1;0} \right).\)
D. \(\left( {0;0} \right).\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(20{\rm{\;cm}}.\)
B. \(\frac{{18}}{{25}}{\rm{\;cm}}.\)
C. \(50{\rm{\;cm}}.\)
D. \(45{\rm{\;cm}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(m = 5.\)
B. \(m = 3.\)
C. \(m = - 3.\)
D. \(m = - 5.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập