Trong không gian \(Oxyz\), gọi \(d\) là đường thẳng đi qua điểm \(A\left( {1; - 1;2} \right)\), song song với mặt phẳng \(\left( P \right):2x - y - z + 3 = 0\), đồng thời tạo với đường thẳng \(\Delta :\frac{{x + 1}}{1} = \frac{{y - 1}}{{ - 2}} = \frac{z}{2}\) một góc lớn nhất. Phương trình đường thẳng \(d\) là    

Gọi \(I\) là giao điểm của 2 cung tròn . Chọn gốc toạ độ \(A\left( {0;0} \right)\) và hệ trục tọa độ \(Axy\) như hình vẽ\( \Rightarrow B\left( {4;0} \right)\).

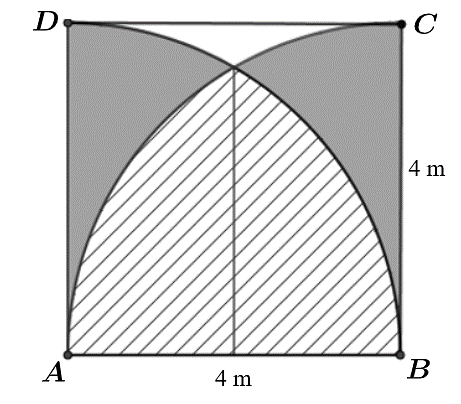
Xét cung tròn có phương trình \(y = \sqrt {16 - {x^2}} \).

Phần diện tích gạch chéo \(S = 2 \cdot \int\limits_2^4 {\sqrt {16 - {x^2}} } {\rm{d}}x = \frac{{16\pi }}{3} - 4\sqrt 3 \) (m²).

Phần diện tích màu xám: \(2 \cdot \left( {\frac{1}{4}\pi \cdot {4^2} - \frac{{16\pi }}{3} + 4\sqrt 3 } \right) = \frac{{ - 8\pi }}{3} + 8\sqrt 3 \) (m²).

Phần diện tích còn lại: \(16 - \left( {\frac{{16\pi }}{3} - 4\sqrt 3 + \frac{{ - 8\pi }}{3} + 8\sqrt 3 } \right) = 16 - \frac{{8\pi }}{3} - 4\sqrt 3 \) (m²).

Số tiền để sơn biển quảng cáo:

\[\left( {\frac{{16\pi }}{3} - 4\sqrt 3 } \right) \cdot 150{\rm{ 000 + }}\left( {\frac{{ - 8\pi }}{3} + 8\sqrt 3 } \right) \cdot 100{\rm{ 000}} + \left( {16 - \frac{{8\pi }}{3} - 4\sqrt 3 } \right) \cdot 250{\rm{ 000}}\, \approx 2\,195\,480\] đồng.

a) Sai. Ta có \(\overrightarrow {AB} = \left( {4; - 4;2} \right)\) nên đoạn thẳng \[AB\] có độ dài bằng \[\sqrt {{4^2} + {4^2} + {2^2}} = 6\].

b) Đúng. Vectơ \[\overrightarrow {AB} = \left( {4; - 4;2} \right) = 2\left( {2; - 2;1} \right)\] nên đường thẳng \[AB\] có phương trình \[\frac{{x - 1}}{2} = \frac{{y - 1}}{{ - 2}} = \frac{z}{1}\].

c) Sai. Vectơ \[\overrightarrow {AC} = \left( { - 1;3; - 1} \right)\] nên khoảng cách từ điểm \[C\] tới đường thẳng \[AB\] bằng

\(d\left( {C,AB} \right) = \frac{{\left| {\left[ {\overrightarrow {AC} ,\overrightarrow {AB} } \right]} \right|}}{{AB}} = \sqrt 2 \).

d) Đúng. Diện tích tam giác \[ABM\] bằng \[\frac{1}{2}AB \cdot d\left( {M,AB} \right) = 6\sqrt 2 \Leftrightarrow d\left( {M,AB} \right) = 2\sqrt 2 \]. Suy ra \(M\) thuộc mặt trụ có trục là đường thẳng \(AB\), bán kính \(R = 2\sqrt 2 \).

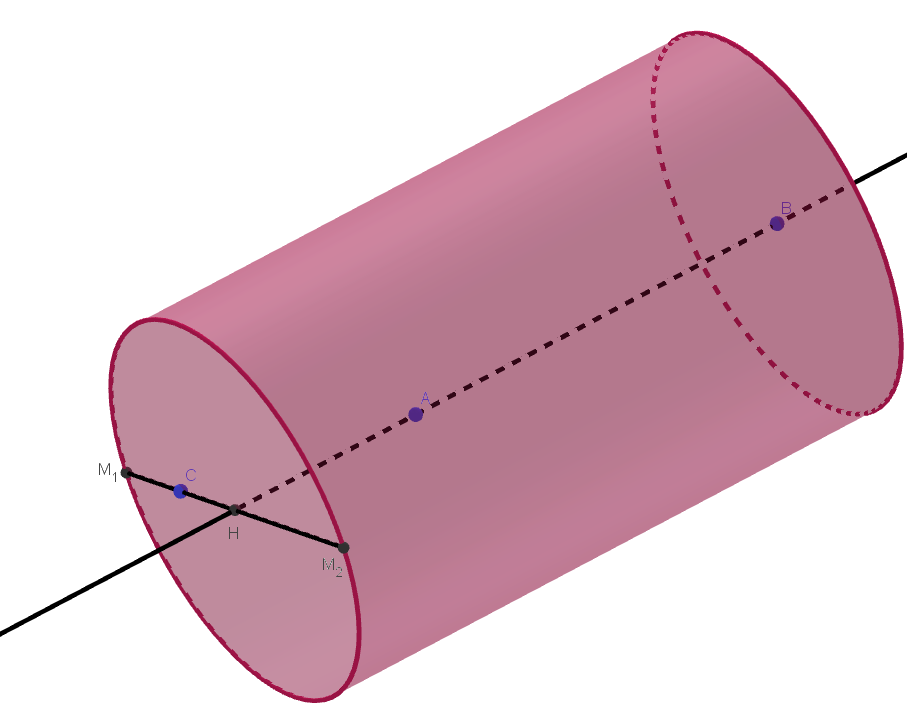
Đoạn thẳng \[MC\] có độ dài nhỏ nhất bằng \[M{C_{\min }} = \left| {d\left( {M,AB} \right) - d\left( {C,AB} \right)} \right| = \sqrt 2 \].