Tại tỉnh X, thống kê cho thấy trong số những người trên 50 tuổi có 7,6% mắc bệnh tim; 11,5% mắc bệnh huyết áp và 4,7% mắc cả bệnh tim và bệnh huyết áp. Từ đó, hãy xác định tỉ lệ dân cư trên 50 tuổi của tỉnh X không mắc cả bệnh tim và bệnh huyết áp là bao nhiêu phần trăm?

Gọi \(h\left( t \right)\) là độ cao của viên đạn bắn lên từ mặt đất sau \(t\) giây kể từ thời điểm đạn được bắn lên.

Khi đó \(h\left( t \right) = \int {v\left( t \right)} \,{\rm{dt}} = \int {\left( {25 - 9,8t} \right)} \,{\rm{dt}} = 25t - 4,9{t^2} + C\,\,\left( {\rm{m}} \right)\).

Do \[h\left( 0 \right) = 1\] nên \(C = 1\) \( \Rightarrow h\left( t \right) = - 4,9{t^2} + 25t + 1\,\,\left( {\rm{m}} \right)\).

Vậy viên đạn đạt độ cao lớn nhất là \(h = - \frac{\Delta }{{4a}} = \frac{{3223}}{{98}}\,\,\left( {\rm{m}} \right)\) khi \(t = - \frac{b}{{2a}} = \frac{{125}}{{49}}\) giây. Chọn B.

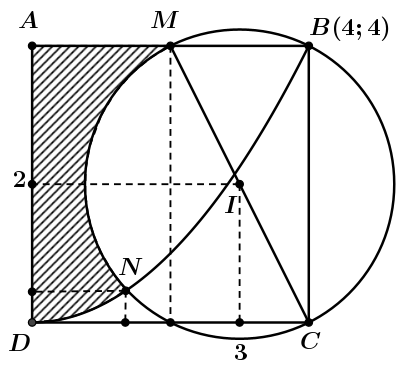
Xét hệ trục tọa độ có gốc tọa độ đặt tại điểm D và tia Ox trùng với tia DC, tia Oy trùng với tia DA.

Parabol \(\left( P \right)\): \(y = a{x^2}\) đi qua \(B\left( {4;4} \right)\) nên \(4 = {4^2} \cdot a \Rightarrow a = \frac{1}{4}\), suy ra \(y = \frac{1}{4}{x^2} \Rightarrow x = 2\sqrt y \).

Ta xác định được \(M\left( {2;4} \right)\) và \(C\left( {4;\,0} \right)\) nên đường tròn có tâm \(I\left( {3;\,2} \right)\) và bán kính \(R = IC = \sqrt {{2^2} + {1^2}} = \sqrt 5 \) có phương trình là \({\left( {x - 3} \right)^2} + {\left( {y - 2} \right)^2} = 5\).

Suy ra \[{\left( {x - 3} \right)^2} = 5 - {\left( {y - 2} \right)^2} \Leftrightarrow 3 - x = \sqrt {5 - {{\left( {y - 2} \right)}^2}} \Leftrightarrow x = 3 - \sqrt {5 - {{\left( {y - 2} \right)}^2}} \].

Phương trình hoành độ giao điểm của \(\left( P \right)\) và đường tròn là: \({\left( {x - 3} \right)^2} + {\left( {\frac{1}{4}{x^2} - 2} \right)^2} = 5\).

\(\left( P \right)\) và đường tròn có hai giao điểm là \(B\left( {4;\,4} \right)\) và \(N\left( {{x_N};\,{y_N}} \right) \Rightarrow \)\({x_N} \approx 1,37 \Rightarrow {y_N} \approx 0,469225\).

Thể tích vật thể cần tính là: \(V = \pi \int\limits_0^{0,469225} {{{\left( {2\sqrt y } \right)}^2}{\rm{d}}y} + \pi \int\limits_{0,469225}^4 {{{\left( {3 - \sqrt {5 - {{\left( {y - 2} \right)}^2}} } \right)}^2}{\rm{d}}y} \approx 14,46\).