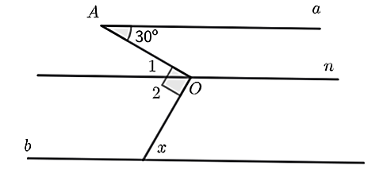
Cho hình dưới đây, biết \[NP\parallel KQ\parallel xy,\,\,\widehat {NPM} = 45^\circ ,\,\,\widehat {KQM} = 135^\circ \].
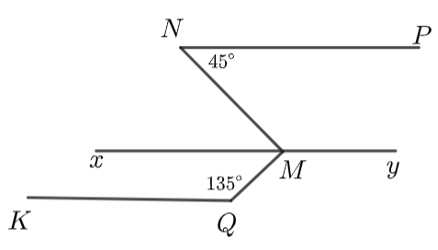
Cho hình dưới đây, biết \[NP\parallel KQ\parallel xy,\,\,\widehat {NPM} = 45^\circ ,\,\,\widehat {KQM} = 135^\circ \].
a) \[\widehat {NMx}\] và \[\widehat {QMx}\] là hai góc kề nhau.
b) \[\widehat {yMQ} = \widehat {KQM} = 135^\circ \] (hai góc đồng vị).
c) \[\widehat {QMx} = 45^\circ \].
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Đúng.
Quan sát hình nhận thấy \[\widehat {NMx}\] và \[\widehat {QMx}\] là hai góc kề nhau.
b) Sai.
Vì \[NP\parallel KQ\parallel xy\] nên \[\widehat {yMQ} = \widehat {KQM} = 135^\circ \] (so le trong).
c) Đúng.
Có \[\widehat {QMx},\,\,\widehat {QMy}\] là hai góc kề bù nên \[\widehat {QMx} + \widehat {QMy} = 180^\circ \].
Do đó, \[\widehat {QMx} = 180^\circ - \widehat {QMy} = 180^\circ - 135^\circ = 45^\circ \].
d) Đúng.
Vì \[NP\parallel KQ\parallel xy\] nên \[\widehat {PNM} = \widehat {NMx} = 45^\circ \].
Ta có: \[\widehat {QMx} + \widehat {xMN} = 45^\circ + 45^\circ = 90^\circ \]. Suy ra \[MN \bot \,QM.\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
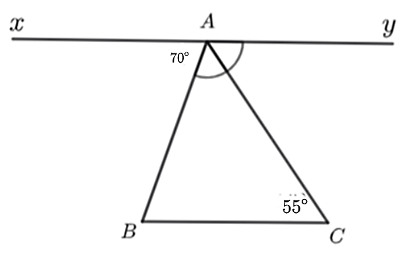
a) \(\widehat {xAB},\widehat {BAC}\) là hai góc kề bù.
b) \(\widehat {BAy} = 110^\circ \).
c) \(\widehat {yAC} = 60^\circ \).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Sai.
Nhận thấy \(\widehat {xAB}\) và \(\widehat {CAB}\) chỉ là hai góc kề nhau do \(\widehat {xAB} + \widehat {CAB} \ne 180^\circ \). Do đó, ý a) sai.
b) Đúng.
Vì tia \(AC\) là tia phân giác của \(\widehat {yAB}\) nên ta có \(\widehat {yAB} = 2\widehat {BAC}\). Do đó, ý b) là đúng.
c) Sai.
Có \(\widehat {xAB}\) và \(\widehat {yAB}\) là hai góc kề là hai góc kề bù nên ta có \(\widehat {xAB} + \widehat {yAB} = 180^\circ \).
Do đó, \(\widehat {yAB} = 180^\circ - \widehat {xAB} = 180^\circ - 70^\circ = 110^\circ \).
Mà tia \(AC\) là tia phân giác của \(\widehat {yAB}\) nên \(\widehat {yAC} = \widehat {CAB} = \frac{{\widehat {yAB}}}{2} = \frac{{110^\circ }}{2} = 55^\circ \).
Vậy ý c) sai.
d) Đúng.
Ta có: \(\widehat {yAC} = 55^\circ \); \(\widehat {ACB} = 55^\circ \) nên \(\widehat {ACB} = \widehat {yAC}\).
Mà hai góc ở vị trí so le trong nên \(xy\parallel BC\).
Do đó, ý d) đúng.
Câu 2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
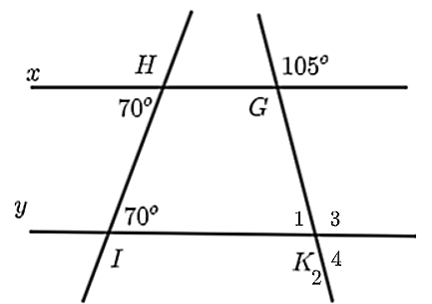
Đáp án đúng là: C
Ta có: \[\widehat {AED} = \widehat {ACB} = 40^\circ \] (giả thiết)
mà hai góc này lại ở vị trí đồng vị
suy ra \[DE\,\parallel \,BC\] (dấu hiệu nhận biết)
suy ra \[\widehat {ADE} = \widehat {ABC}\] (đồng vị) (1)
Ta lại có: \[\widehat {ADE} + \widehat {EDB} = 180^\circ \] (hai góc kề bù)
Suy ra \[\widehat {ADE} + 105^\circ = 180^\circ \], do đó \[\widehat {ADE} = 180^\circ - 105^\circ = 75^\circ \] (2)
Từ (1) và (2) suy ra \[\widehat {ABC} = 75^\circ \].
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
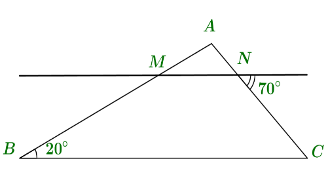
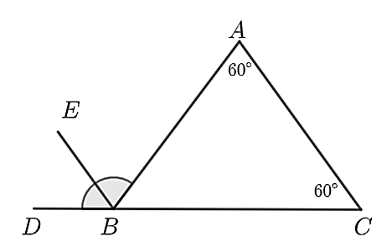
a) \[\widehat {DBA}\] là góc ngoài tại đỉnh \[B\] của tam giác \[ABC\].
b) Tam giác \[ABC\] là tam giác vuông tại \[B.\]
c) \[\widehat {DBA} = \widehat C + \widehat A\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập