Vẽ hình theo diễn đạt sau (vẽ trên cùng một hình).
a) Vẽ đoạn thẳng \[AB\] có độ dài 6 cm và trung điểm \[C\] của đoạn thẳng đó. Tính độ dài đoạn thẳng \[CA\].
b) Vẽ đường thẳng \[d\] cắt đoạn thẳng \[AB\] tại điểm \[C\]. Trên đường thẳng \[d\] lấy hai điểm \[E\] và \[F\] sao cho điểm \[C\] nằm giữa \[E\] và \[F\].
c) Điểm \[C\] là mút chung của những đoạn thẳng nào?
Vẽ hình theo diễn đạt sau (vẽ trên cùng một hình).
a) Vẽ đoạn thẳng \[AB\] có độ dài 6 cm và trung điểm \[C\] của đoạn thẳng đó. Tính độ dài đoạn thẳng \[CA\].
b) Vẽ đường thẳng \[d\] cắt đoạn thẳng \[AB\] tại điểm \[C\]. Trên đường thẳng \[d\] lấy hai điểm \[E\] và \[F\] sao cho điểm \[C\] nằm giữa \[E\] và \[F\].
c) Điểm \[C\] là mút chung của những đoạn thẳng nào?
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 6 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
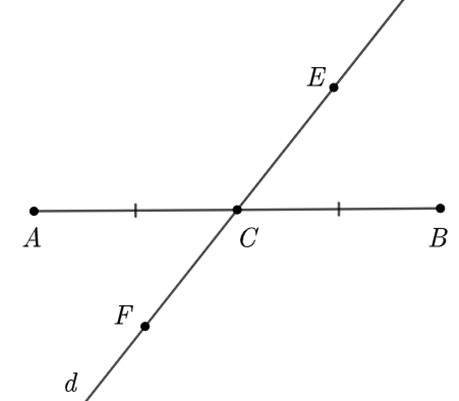
a) Cách vẽ đoạn thẳng \[AB = 6\] cm và trung điểm \[C\] của đoạn thẳng \(AB\) như sau:
• Chọn điểm \[A\] bất kỳ, dùng thước thẳng có chia vạch có đơn vị cm và đặt thước sao cho vạch 0 trùng với điểm \[A\].
• Tại vạch số 6 cm của thước ta có điểm \[B\] và nối \[A\] với \[B\] ta được đoạn thẳng \[AB = 6\] cm.
• Dùng thước có chia vạch chọn điểm giữa đoạn thẳng \[AB\] thành hai đoạn bằng nhau ta được điểm \[C\] là trung điểm của đoạn \[AB\].
Vì \[C\] là trung điểm của đoạn thẳng \[AB\] nên \(CA = CB = \frac{{AB}}{2}\).
Mà ta có độ dài \[AB = 6\] cm.
Độ dài đoạn thẳng \[CA\] là: \[6:2 = 3\] (cm).
Vậy \[CA = 3\] cm.
b) Đặt thước thẳng tại \[C\] sao cho vẽ một đường thẳng bất kỳ nhưng không trùng với đoạn thẳng \[AB\] ta được đường thẳng \[d\] cắt đoạn thẳng \[AB\].
Lấy điểm \[E\] bất kỳ nằm trên đường thẳng \[d\] (về phía trên đoạn \[AB\]) và \[F\] nằm trên tia đối của \[CE\], khi đó \[C\] nằm giữa hai điểm \[E\] và \[F\].
c) Các đoạn thẳng có điểm mút chung \[C\] bao gồm \[CA,{\rm{ }}CB,{\rm{ }}CE,\,\,CF.\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có \(F = \frac{1}{{18}} + \frac{1}{{54}} + \frac{1}{{108}} + ... + \frac{1}{{990}}\)
\( = \frac{1}{{3.6}} + \frac{1}{{6.9}} + \frac{1}{{9.12}} + ... + \frac{1}{{30.33}}\)
\( = \frac{1}{3}.\left( {\frac{3}{{3.6}} + \frac{3}{{6.9}} + \frac{3}{{9.12}} + ... + \frac{3}{{30.33}}} \right)\)
\( = \frac{1}{3}.\left( {\frac{{6 - 3}}{{3.6}} + \frac{{9 - 6}}{{6.9}} + \frac{{12 - 9}}{{9.12}} + ... + \frac{{33 - 30}}{{30.33}}} \right)\)
\( = \frac{1}{3}.\left[ {\left( {\frac{6}{{3.6}} - \frac{3}{{3.6}}} \right) + \left( {\frac{9}{{6.9}} - \frac{6}{{6.9}}} \right) + \left( {\frac{{12}}{{9.12}} - \frac{9}{{9.12}}} \right) + ... + \left( {\frac{{33}}{{30.33}} - \frac{{30}}{{30.33}}} \right)} \right]\)
\( = \frac{1}{3}.\left( {\frac{1}{3} - \frac{1}{6} + \frac{1}{6} - \frac{1}{9} + \frac{1}{9} - \frac{1}{{12}} + ... + \frac{1}{{30}} - \frac{1}{{33}}} \right)\)
\( = \frac{1}{3}.\left( {\frac{1}{3} - \frac{1}{{33}}} \right)\)\( = \frac{1}{3}.\frac{{10}}{{33}} = \frac{{10}}{{99}}\).
Vậy \(F = \frac{{10}}{{99}}\).
Lời giải
a) Phân số biểu thị diện tích phần lát gạch là :
\[1 - \frac{1}{5} = \frac{4}{5}\] (diện tích sân vườn)
Diện tích sân vườn là: \[36:\frac{4}{5} = 45\] (m2)
b) Diện tích đất trồng cỏ là: \[45 - 36 = 9\] (m2)
Số tiền mua 9 m2 cỏ là: \[9\,.\,50\,\,000 = 450\,\,000\] (đồng).
Vậy số tiền mua 9 m2 cỏ là \[450\,\,000\] đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
