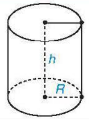
Thay dấu “\[?\]”bằng giá trị thích hợp và hoàn thành bảng sau:

Hình trụ	Bán kính đáy (cm)	Chiều cao (cm)	Diện tích xung quanh (cm2)	Diện tích toàn phần (cm2)	Thể tích (cm3)
	\[3\]	\[7\]	\[?\]	\[?\]	\[?\]
	\[4\]	\[?\]	\[20\pi \]	\[?\]	\[?\]
	\[?\]	\[8\]	\[?\]	\[18\pi \]	\[?\]
	\[?\]	\[5\]	\[?\]	\[?\]	\[150\pi \]

· Với \[r = 3,h = 7\]

\[{S_{xq}} = 2\pi rh = 42\pi \left( {c{m^2}} \right)\]

\[{S_{tp}} = 2\pi r\left( {h + r} \right) = 60\pi \left( {c{m^2}} \right)\]

\[V = \pi {r^2}h = 63\pi \left( {c{m^3}} \right)\]

· Với \[r = 3,{S_{xq}} = 20\pi \left( {c{m^2}} \right)\]

\[{S_{xq}} = 2\pi rh \Rightarrow h = \frac{{{S_{xq}}}}{{2\pi r}} = 2,5\left( {cm} \right)\]

\[{S_{tp}} = 2\pi r\left( {h + r} \right) = 52\pi \left( {c{m^2}} \right)\]

\[V = \pi {r^2}h = 40\pi \left( {c{m^3}} \right)\]

· Với \[h = 8,{S_{xq}} = 18\pi \left( {c{m^2}} \right)\]

\[\begin{array}{l}{S_{tp}} = 2\pi r\left( {h + r} \right)\\18\pi  = 2\pi r\left( {h + r} \right)\\{r^2} + 8r - 9 = 0\\ \Rightarrow r = 1\end{array}\]

\[{S_{xq}} = 2\pi rh = 16\pi \left( {c{m^2}} \right)\]

\[V = \pi {r^2}h = 8\pi \left( {c{m^3}} \right)\]

· Với \[h = 5,V = 150\pi \]

\[V = \pi {r^2}h \Rightarrow h = \frac{V}{{\pi {r^2}}} = \frac{{150\pi }}{{25\pi }} = 6\left( {cm} \right)\]

\[{S_{xq}} = 2\pi rh = 60\pi \left( {c{m^2}} \right)\]

\[{S_{tp}} = 2\pi r\left( {h + r} \right) = 110\pi \left( {c{m^2}} \right)\]