Cho tam giác \(ABC\) vuông tại \(A\), \(AB = 6cm,\,AC = 8cm\). Gọi \({V_1}\) là thể tích hình nón tạo thành khi quay tam giác \(ABC\) quanh cạnh \(AB\) và \({V_2}\) là thể tích hình nón tạo thành khi quay tam giác \(ABC\) quanh cạnh \(AC\). Tính tỷ số \[\frac{{{V_1}}}{{{V_2}}}\].
Quảng cáo
Trả lời:
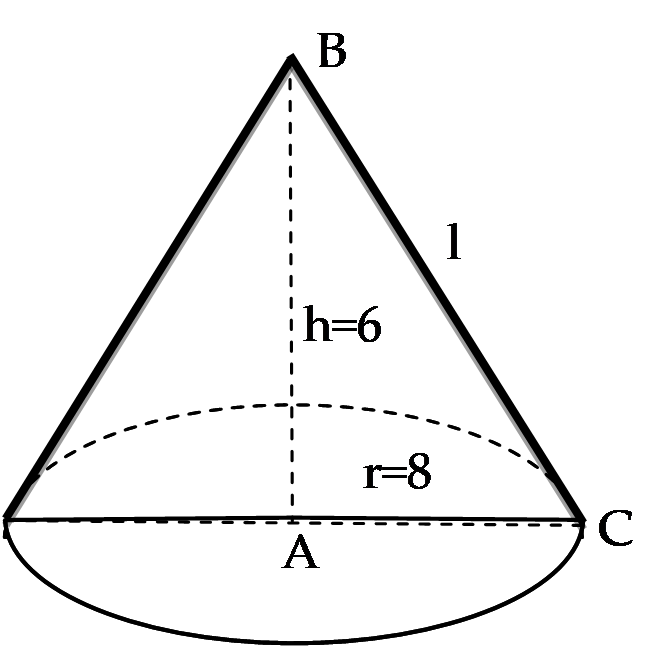
Ta có công thức tính thể tích hình nón có chiều cao \(h\) và bán kính \(r\) là \(V = \frac{1}{3}\pi {r^2}h\)
+ Khi quay tam giác \(ABC\) quanh cạnh \(AB\) thì:
\(h = AB = 6cm\) và \(r = AC = 8cm\) thì \({V_1} = \frac{1}{3}\pi {.8^2}.6 = 128\pi \)
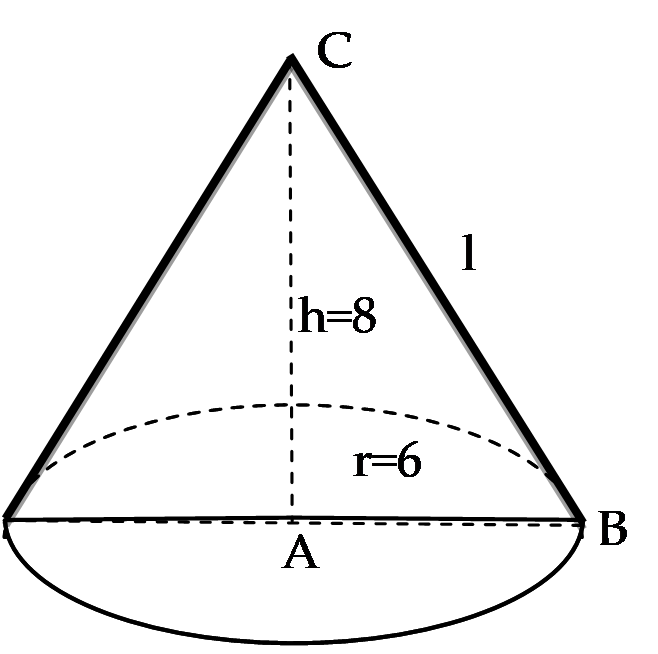
+ Khi quay tam giác \(ABC\) quanh cạnh \(AC\) thì:
\(h = AC = 8cm\) và \(r = AB = 6cm\) thì \({V_2} = \frac{1}{3}\pi {.6^2}.8 = 96\pi \)
Vậy: \[\frac{{{V_1}}}{{{V_2}}} = \frac{4}{3}\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
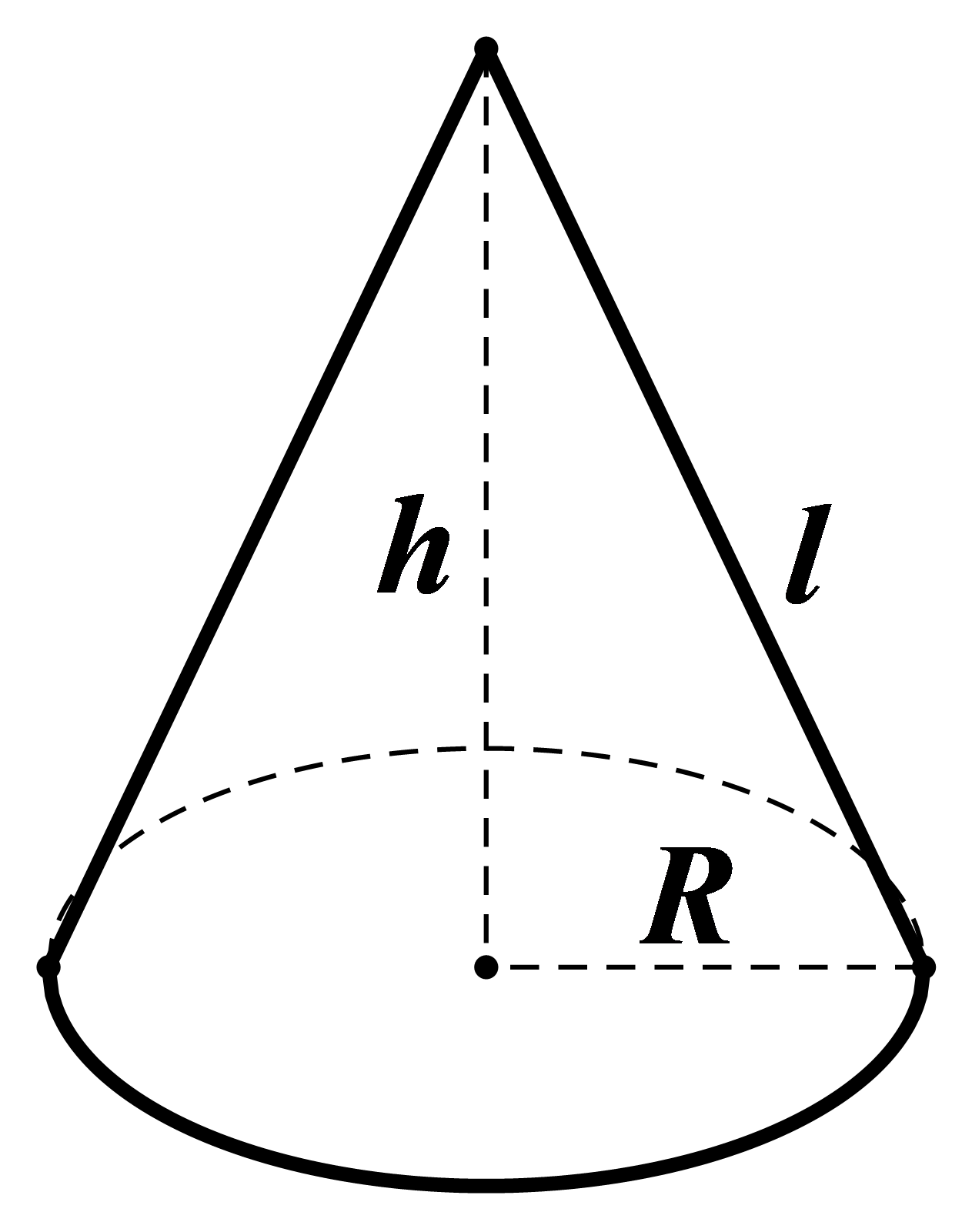
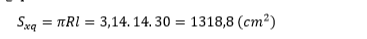
Vậy diện tích lá dùng để làm nón là 110%.1318,8=1450,68 cm2
Lời giải
Vì chiếc nón hình nón có đường sinh l = 30cm và bán kính đáy R = 40: 2 = 20cm nên diện tích xung quanh của chiếc nón là:
Sxq = pRl = p. 20. 30 = 600p (cm2)
diện tích là cần dùng cho một chiếc nón là: 2. 600p = 1200p cm2.
Vậy diện tích là cần dùng làm 5000 chiếc nón là: 500. 1200p = 600000p cm2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.


