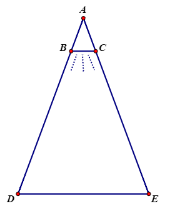
Một chóa đèn có dạng hình nón với đường kính đáy BC=20cm, đặt bên trong là một bóng đèn tại A. Khi được treo trên trần nhà thì đèn chiếu sáng một khoảng rộng 3m trên nền nhà. Biết rằng độ cao từ trần nhà ( điểm A) là 4,2 m. Tính:

a) Khoảng hở giữa chóa đèn và nền nhà?

b) Diện tích được chiếu sáng trên nền nhà (Biết bóng đèn chiếu sáng trên nền nhà là một hình tròn)

                   

a) Khi quay tam giác \[R = HC = 2\] xung quanh trục \(\Delta AHC\), ta thu được hình nón có bán kính đáy \(r = AC = a\), chiều cao \(h = AB = a\sqrt 3 \)và đường sinh là cạnh huyền \(l = BC\).

Xét tam giác \( = 2\sqrt 3 \) vuông tại \(V = \frac{1}{3}\pi {R^2}.AH\), theo pythagore, ta có:

\[\begin{array}{l}B{C^2} = A{C^2} + A{B^2} = 2{a^2}\\ \Rightarrow BC = 2a \Rightarrow l = 2a\end{array}\]

Đường sinh của hình nón \[2a\] (đvđd)

b) Thể tích hình nón là: \[V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi .{a^2}.a\sqrt 3  = \frac{{{a^3}\sqrt 3 \pi }}{3}\] (đvtt)

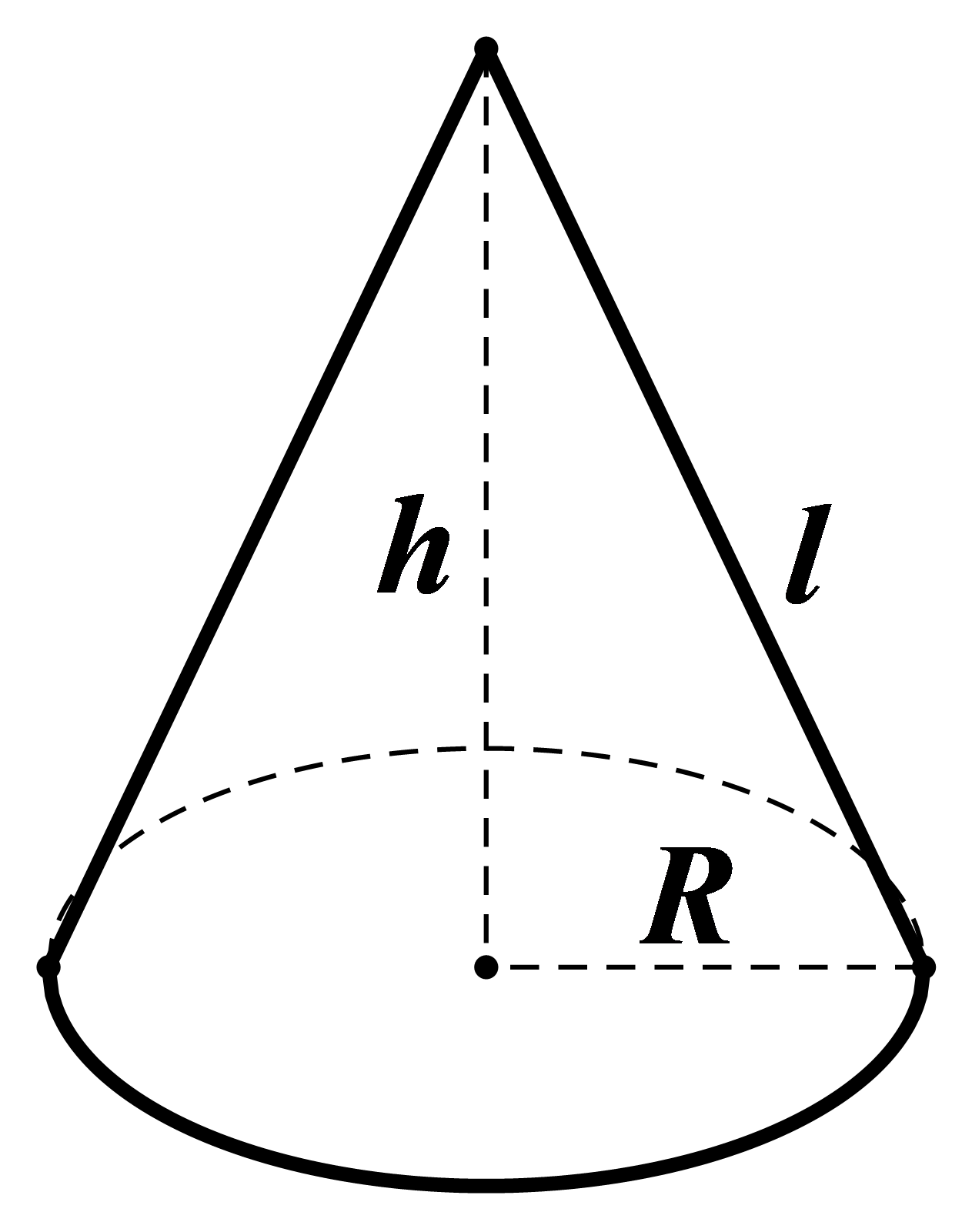
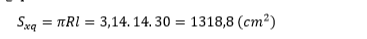
Vậy diện tích lá dùng để làm nón là 110%.1318,8=1450,68 cm²