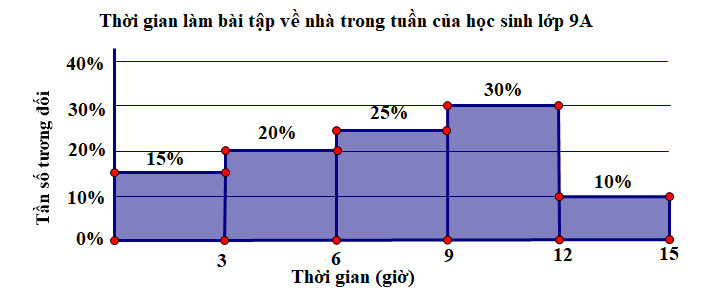
Cho bảng tần số tương đối ghép nhóm về thời gian làm bài tập về nhà trong tuần (đơn vị tính là giờ) của 40 bạn học sinh lớp 9A.

Thời gian (giờ)	\(\left[ {0;3} \right)\)	\(\left[ {3;6} \right)\)	\(\left[ {6;9} \right)\)	\(\left[ {9;12} \right)\)	\(\left[ {12;15} \right)\)
Tần số tương đối	\(15{\rm{\% }}\)	\(20{\rm{\% }}\)	\(25{\rm{\% }}\)	\(30{\rm{\% }}\)	\(10{\rm{\% }}\)

a) Tính tỉ lệ học sinh trong lớp dành ít nhất 6 giờ trong tuần để làm bài tập về nhà.

b) Có bao nhiêu học sinh lớp 9 A dành ít nhất 6 giờ trong tuần để làm bài tập về nhà?

c) Vẽ biểu đồ tần số tương đối ghép nhóm dạng cột biểu diễn bảng tần số tương đối ghép nhóm trên.

Bác Ba ghi lại thời gian truy cập Internet của mình mỗi ngày (đơn vị: giờ) trong vòng 1 tháng như sau:

    Bác Ba đánh giá mức độ sử dụng Internet mỗi ngày của mình theo bảng tiêu chí sau:

    Hãy lập bảng tần số ghép nhóm và bảng tần số tương đối ghép nhóm cho dữ liệu về thời gian truy cập Internet của bác Quảng, trong đó các nhóm được phân theo mức độ sử dụng như bảng tiêu chí trên.

a) Đọc và giải thích thông tin của hai nhóm dữ liệu cho bởi bảng tần số tương đối ghép nhóm trên.

b) Lập bảng tần số ghép nhóm cho kết quả 20 lần đo của nhóm học sinh.

Mẫu số liệu dưới đây ghi lại tốc độ (đơn vị: \(\left[ {40;70} \right)\) ) của \(44\) ô tô khi đi qua một trạm đo tốc độ:

\[\begin{array}{*{20}{l}}{48,5}&{43}&{50}&{55}&{45}&{60}&{53}&{55,5}&{44}&{65}&{54,5}\\{51}&{62,5}&{41}&{44,5}&{57}&{57}&{68}&{49}&{46,5}&{53,5}&{49}\\{61}&{49,5}&{54}&{62}&{59}&{56}&{47}&{50}&{59,5}&{61}&{46,5}\\{49,5}&{52,5}&{57}&{47}&{59}&{55}&{45}&{47,5}&{48}&{61,5}&{48,5}\end{array}\]

    Hãy ghép các số liệu thành sáu nhóm ứng với sáu nửa khoảng có độ dài bằng nhau?

Một công ty quản lý phần mềm ứng dưng trực tuyến đã thống kê tỉ lệ người dùng phần mềm này theo dung lượng bộ nhớ dành cho lưu trữ ảnh và biểu diễn dưới dạng biểu đồ tần số tương đối ghép nhóm dạng cột như sau:

Một phòng khám đo và ghi lại huyết áp tâm thu (đơn vị tính là \(mmHg\)) của một số người đến khám bệnh thu được kết quả như sau:

Theo Hiệp hội Tim mạch Hoa Kỳ, người bình thường có huyết áp tâm thu từ \(90mmHg\) đến dưới \(120mmHg\) , người ở dạng tiền tăng huyết áp có huyết áp tâm thu từ \(120mmHg\) đến dưới \(140mmHg\) ; người bị tăng huyết áp có huyết áp tâm thu lớn hơn hoặc bằng \(140mmHg\) .

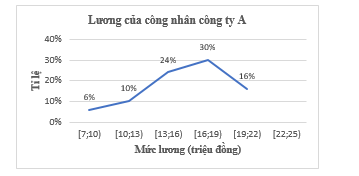
Lập bảng tần số ghép nhóm và bảng tần số tương đối ghép nhóm cho dãy số liệu trên theo các mức bệnh huyết áp.