Có hai bình cách nhiệt. Bình I chứa 5 lít nước ở \({60^\circ }{\rm{C}}\), bình II chứa 1 lít nước ở \({20^\circ }{\rm{C}}\). Đầu tiên, rót một phần nước ở bình I sang bình II. Sau khi bình II cân bằng nhiệt, người ta lại rót từ bình II sang bình I một lượng nước bằng với lần rót trước. Nhiệt độ sau cùng của nước trong bình I là \({59^\circ }{\rm{C}}\). Lượng nước đã rót từ bình này sang bình kia mỗi lần là
Câu hỏi trong đề: Đề thi thử tốt nghiệp THPT môn Vật lí Đà Nẵng có đáp án !!
Quảng cáo
Trả lời:
Gọi lượng nước đã rót từ bình này sang bình kia mỗi lần là x (lít)
Cân bằng nhiệt ở bình II có x . c. \((60 - t) = 1.c.(t - 20) \Rightarrow t = \frac{{60x + 20}}{{1 + x}}\)
Cân bằng nhiệt ở bình I có \((5 - x).c.(60 - 59) = x.c.(59 - t) \Rightarrow t = \frac{{60x - 5}}{x}\)
Từ (1) và (2) \( \Rightarrow {\rm{x}} = 1/7\) (lít). Chọn \({\bf{B}}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Khối lượng của nước đá lớn hơn rất nhiều khối lượng của bi nên khi có sự cân bằng nhiệt thì nhiệt độ là \({0^\circ }{\rm{C}}\).
Thể tích viên bi sắt (hình cầu) là \({V_s} = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi \cdot {6^3} = 288\pi \;{\rm{c}}{{\rm{m}}^3} = 288\pi \cdot {10^{ - 6}}\;{{\rm{m}}^3}\)
Khối lượng viên bi sắt là \({m_s} = {D_s}{V_s} = 7800 \cdot 288\pi \cdot {10^{ - 6}} = 2,2464\pi (\;{\rm{kg}})\)
Nhiệt lượng mà viên bi tỏa ra để hạ xuống \({0^\circ }{\rm{C}}\) là:
\(Q = {m_s}{c_s}\Delta {t_s} = 2,2464\pi \cdot 460 \cdot 325 = 335836,8\pi (\;{\rm{J}})\)
Khối lượng nước đá tan thành nước là \({m_0} = \frac{Q}{\lambda } = \frac{{335836,8\pi }}{{3,{{4.10}^5}}}(\;{\rm{kg}})\)
Thể tích khối đá tan ra là \(V = \frac{{{m_0}}}{{{D_0}}} = \frac{{\frac{{335836,8\pi }}{{3,{{4.10}^5}}}}}{{915}} \approx 3,{39.10^{ - 3}}\;{{\rm{m}}^3}\)
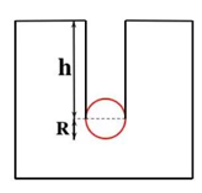
Do V là tổng thể tích của một hình trụ có chiều cao là h và một nửa hình cầu bán kính R nên ta có \(V = \pi {R^2}h + \frac{{{V_s}}}{2} \Rightarrow 3,39 \cdot {10^{ - 3}} = \pi \cdot 0,{06^2} \cdot h + \frac{{288\pi \cdot {{10}^{ - 6}}}}{2} \Rightarrow h \approx 0,26m = 26\;{\rm{cm}}\)
Viên bi chui vào nước đá đến độ sâu là \(h + R = 26 + 6 = 32\;{\rm{cm}}\). Chọn \({\bf{A}}\)
Câu 2
Lời giải
a) Đúng
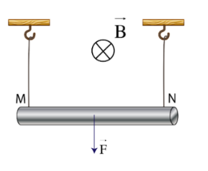
b) Đúng. Từ thông qua vòng dây biến thiên nên xuất hiện suất điện động cảm ứng
c) Sai. Chu kì không thay đổi.
d) Đúng. Dòng điện cảm ứng sẽ sinh ra lực từ chống lại chuyển động của vòng dây, cơ năng sẽ chuyển hóa thành nhiệt lượng tỏa ra trên vòng dây.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.