Cho vòng quay mặt trời gồm mười hai cabin như vẽ bên dưới. Hỏi để cabin \(A\) di chuyển đến vị trí cao nhất thì vòng quay phải quay thuận chiều kim đồng hồ quanh tâm bao nhiêu độ?
Câu hỏi trong đề: 11 bài tập Toán 9 Cánh diều Bài 2. Phép quay có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Vì vòng quay mặt trời gồm mười hai cabin nên hai cabin liền kề cách nhau một góc bằng: \(360^\circ :12 = 30^\circ \)
Do vậy để cabin \(A\) di chuyển đến vị trí cao nhất thì vòng quay thuận chiều kim đồng hồ quanh tâm một góc bằng: \(30^\circ .4 = 120^\circ \)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
![Cho hình ngũ giác đều \(ABCDE\) có tâm \(O\). a) Phép quay thuận chiều tâm \(O\) biến điểm \(A\) thành điểm \[C\] thì các điểm \(B,C,D,E\) tương ứng biến thành các điểm nào? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/17-1769711223.png)
a) \(\widehat {AOC} = \frac{{360^\circ }}{5}.2 = 144^\circ \)
Phép quay thuận chiều \(144^\circ \) tâm \(O\) biến điểm \(A\) thành điểm \[C\] thì các điểm \(B,C,D,E\) tương ứng biến thành các điểm \[D,E,A,B\]
b) Các phép quay tâm \(O\) giữ nguyên hình ngũ giác đều đã cho là:
⦁ Năm phép quay thuận chiều \[\alpha ^\circ \] tâm \[O\] với \[\alpha ^\circ \]lần lượt nhận các giá trị\[72^\circ ;144^\circ ;216^\circ ;288^\circ ;360^\circ \] .
⦁ Năm phép quay ngược chiều \[\alpha ^\circ \] tâm \[O\] với \[\alpha ^\circ \] lần lượt nhận các giá trị \[72^\circ ;144^\circ ;216^\circ ;288^\circ ;360^\circ \]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
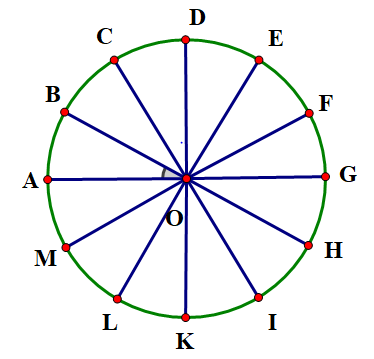
Đa giác đều 12 cạnh \[ABCDEFGHIKLM\] nội tiếp đường tròn \(\left( O \right)\) (Xem hình vẽ).
Ta có: và
Và \(OA = OB = OC = OD = \ldots \) (bán kính đường tròn ngoại tiếp)
Ta chọn phép quay thuận chiều (hoặc ngược chiều) góc quay biến đa giác đã cho thành chính nó.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập