Khi khảo sát một nhóm gồm 40 học sinh lớp 6 về việc học môn toán đã cho kết quả gồm ba loại như sau: 60% học sinh thích học toán, số học sinh thấy việc học toán cũng bình thường bằng \(\frac{1}{2}\) số học sinh thích học toán; còn lại là các học sinh không thích và sợ học toán.
a) Tính số học sinh mỗi loại trong nhóm được khảo sát.
b) Tính số phần trăm giữa số học sinh không thích và sợ học toán so với tổng số học sinh được khảo sát.
Khi khảo sát một nhóm gồm 40 học sinh lớp 6 về việc học môn toán đã cho kết quả gồm ba loại như sau: 60% học sinh thích học toán, số học sinh thấy việc học toán cũng bình thường bằng \(\frac{1}{2}\) số học sinh thích học toán; còn lại là các học sinh không thích và sợ học toán.
a) Tính số học sinh mỗi loại trong nhóm được khảo sát.
b) Tính số phần trăm giữa số học sinh không thích và sợ học toán so với tổng số học sinh được khảo sát.
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 6 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
a) Số học sinh thích học môn toán là:
\[40\,.{\rm{ }}60\% = 24\] (học sinh);
Số học sinh thấy việc học môn toán cũng bình thường là:
\(24\,\,.\,\,\frac{1}{2} = 12\) (học sinh)
Số học sinh không thích và sợ học toán là:
\[40--24--12 = 14\] (học sinh).
b) Tỉ số phần trăm giữa số học sinh không thích và sợ học toán so với tổng số học sinh được khảo sát là:
\(\frac{{14}}{{40}}\,\,.\,\,100 = 56\% \).
Vậy tỉ số phần trăm giữa số học sinh không thích và sợ học toán so với tổng số học sinh được khảo sát là 56%.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án đúng là: B
Phân số có dạng \(\frac{a}{b}\) với \[a,\,\,b \in \mathbb{Z};\,\,b \ne 0\].
Do đó, cách viết \(\frac{{ - \,4}}{5}\) là cách viết phân số.
Câu 2
Lời giải
Đáp án đúng là: D
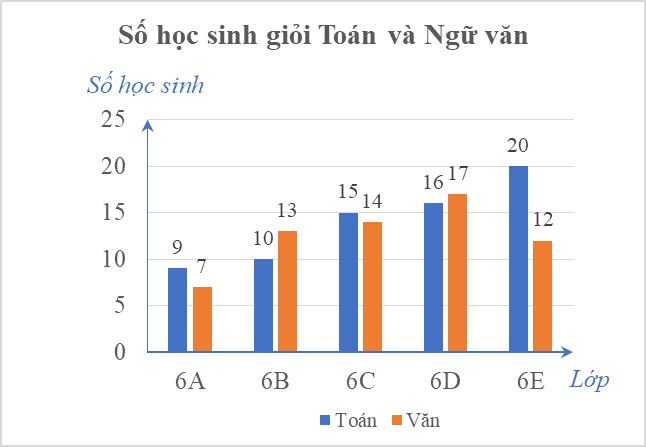
Quan sát biểu đồ, số học sinh giỏi Ngữ văn ở các lớp 6 được biễu diễn bằng các hình chữ nhật màu trắng.
So sánh độ cao các cột màu trắng, ta thấy lớp có số học sinh giỏi Ngữ văn nhiều nhất là lớp 6E.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.