I. PHẦN TRẮC NGHIỆM KHÁCH QUAN
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây.
Phần tô màu trong hình sau biểu diễn phân số nào?

I. PHẦN TRẮC NGHIỆM KHÁCH QUAN
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây.
Phần tô màu trong hình sau biểu diễn phân số nào?

Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 6 Chân trời sáng tạo có đáp án !!
Quảng cáo
Trả lời:

Đáp án đúng là: D
Trong hình vẽ tổng số ô vuông là 12, với số ô vuông được tô màu là 8.
Vậy phân số chỉ phần tô màu trong hình vẽ là \[\frac{8}{{12}} = \frac{{2\,.\,4}}{{3\,.\,4}} = \frac{2}{3}\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
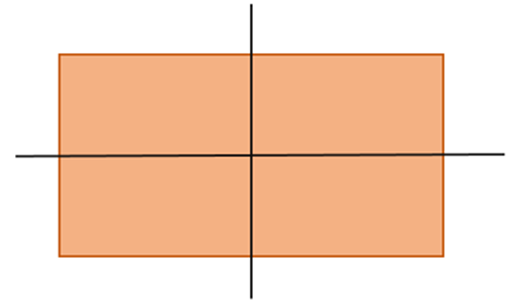
1. • Hình chữ nhật có hai trục đối xứng chia hình chữ nhật thành hai phần (như hình vẽ).
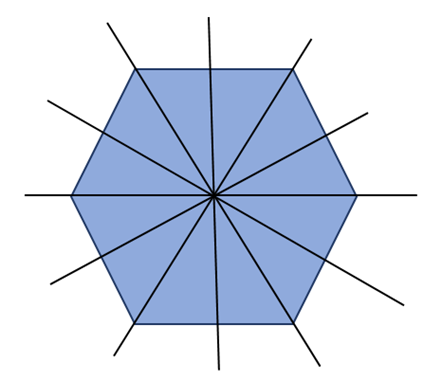
• Hình lục giác đều có 6 trục đối xứng là các đường thẳng lần lượt chia hình lục giác thành hai nửa (như hình vẽ).
2.
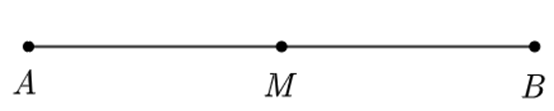
a) Theo đề bài ta có hai điểm \[M\] và \[B\] thuộc tia \[AB\].
Mà độ dài đoạn thẳng \[AB = 6\] cm và \[AM = 3\] cm, suy ra \[AM < AB\].
Vậy điểm \[M\] nằm giữa hai điểm \[A\] và \[B\].
b) Vì điểm \[M\] nằm giữa hai điểm \[A\] và \[B\] nên:
\[AM + MB = AB\] với \[AB = 6\] cm và \[AM = 3\] cm;
Độ dài đoạn thẳng \[MB\] là: \[MB = AB--AM = 6--3 = 3\] (cm).
Suy ra: \[AM = MB = 3\] cm.
* Điểm \[M\] là trung điểm của đoạn thẳng \[AB\] vì:
• Điểm \[M\] nằm giữa hai điểm \[A\] và \[B\];
• \[AM = MB\].
Lời giải
a) Số trang sách bạn An đọc được trong ngày thứ nhất là:
\[120\,\,.\,\,\frac{2}{5} = 48\] (trang)
Vậy ngày thứ nhất bạn An đọc được 48 trang sách.
b) Sau ngày thứ nhất, số trang sách còn lại là:
\[120 - 48 = 72\] (trang);
Số trang sách ngày thứ hai bạn An đọc được là:
\[72\,\,.\,\,\frac{2}{3} = 48\] (trang);
Số trang sách bạn An đọc trong ngày thứ ba là:
\[72--48 = 24\] (trang).
Vậy trong ngày thứ ba bạn An đọc được 24 trang.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.