Bạn An đang làm đề ôn tập theo ba mức độ dễ, trung bình và khó. Xác suất để An hoàn thành câu dễ là \(0,8\); hoàn thành câu trung bình là \(0,6\) và hoàn thành câu khó là \(0,15\). Làm đúng mỗi một câu dễ An được \(0,1\) điểm, làm đúng mỗi một câu trung bình An được \(0,25\) điểm và làm đúng mỗi một câu khó An được \(0,5\) điểm.

 

Đáp án: \(23,4\).

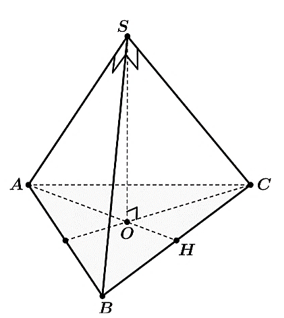
Xét hình chóp tam giác đều \(S.ABC\) trong đó \(S\)  là đỉnh của hình lập phương nằm bên trong ly nước và \(A,\,B,\,C\) là các điểm chung của hình lập phương với miệng ly; \(O\) là trọng tâm tam giác \(ABC\)và \(H\) là trung điểm \(BC\).

Đặt \(x\)(cm) là cạnh đáy hình chóp thì \(AO = \frac{2}{3}AH = \frac{2}{3} \cdot \frac{{x\sqrt 3 }}{2} = \frac{{x\sqrt 3 }}{3}\).

Vì hình chóp \[S.ABC\]có\[SA\], \[SB\], \[SC\]bằng nhau và đôi một vuông góc tại đỉnh \[S\] nên độ dài cạnh \(SA = SB = SC = \frac{x}{{\sqrt 2 }}\).

Từ đó suy ra \(SO = \sqrt {S{A^2} - O{A^2}} = \sqrt {\frac{{{x^2}}}{2} - \frac{{{x^2}}}{3}} = \frac{{x\sqrt 6 }}{6}\).

Theo giả thiết thì chiều cao hình chóp S.ABC bằng \(\frac{1}{3}\) chiều cao ly nước: \(SO = \frac{1}{3}.9 = 3\)(cm).

Suy ra chiều dài cạnh đáy của hình chóp: \(\frac{{x\sqrt 6 }}{6} = 3 \Rightarrow x = 3\sqrt 6 \)(cm).

Vậy thể tích nước tràn ra bằng với thể tích khối chóp \(S.ABC\).

Thể tích đó là: \(V = \frac{1}{3}SO.{S_{ABC}} = \frac{1}{3}.3.\frac{{{{\left( {3\sqrt 6 } \right)}^2}\sqrt 3 }}{4} = \frac{{27\sqrt 3 }}{2} \approx 23,4\)(cm³).

Đáp án: 0,45.

Xét các biến cố \(A\): “lấy được viên bi đỏ của hộp I”.

\(B\): “lấy được viên bi đỏ của hộp II”.

\(C\): “lấy được viên bi đỏ của hộp III”.

Xác suất lấy được viên bi đỏ của hộp I: \(P\left( A \right) = \frac{a}{{a + 2}}\).

Xác suất lấy được viên bi đỏ của hộp II: \(P\left( B \right) = \frac{b}{{b + 3}}\).

Xác suất lấy được viên bi đỏ của hộp III: \(P\left( C \right) = \frac{6}{{6 + 4}} = 0,6\).

Gọi biến cố \(D\): “lấy ra ít nhất một viên bi đỏ” \( \Rightarrow \overline D \): “lấy ra được 3 viên bi xanh”.

\( \Rightarrow P\left( {\overline D } \right) = 1 - P\left( D \right) = 0,024\)

\( \Leftrightarrow \frac{2}{{a + 2}}.\frac{3}{{b + 3}}.\frac{4}{{10}} = 0,024 \Leftrightarrow \left( {a + 2} \right)\left( {b + 3} \right) = 100\)(1).

Xác suất lấy được cả 3 viên bi đỏ \(P\left( A \right).P\left( B \right).P\left( C \right) = 0,336 \Leftrightarrow \frac{a}{{a + 2}}.\frac{b}{{b + 3}}.0,6 = 0,336\).

\( \Leftrightarrow ab = 56\) (2)

Từ (1) và (2) \( \Rightarrow \left\{ \begin{array}{l}a = 8\\b = 7\end{array} \right.\) (vì \(a,b\) là số nguyên).

Xác suất lấy được đúng 2 viên đỏ:

\(P\left( A \right).P\left( B \right).P\left( {\overline C } \right) + P\left( A \right).P\left( {\overline B } \right).P\left( C \right) + P\left( {\overline A } \right).P\left( B \right).P\left( C \right)\)

                                                        \( = 0,8.0,7.0,4 + 0,8.0,3.0,6 + 0,2.0,7.0,6 = 0,452 \simeq 0,45\).