Cho hàm số \(f(x) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình sau đây.
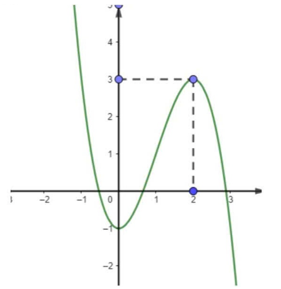
Số nghiệm dương của phương trình \(2f(x) - 3 = 0\) là:
Quảng cáo
Trả lời:
Chọn D
1. Biến đổi phương trình:
\(2f(x) - 3 = 0 \Leftrightarrow 2f(x) = 3 \Leftrightarrow f(x) = \frac{3}{2} = 1.5\)
Số nghiệm của phương trình chính là số giao điểm của đồ thị hàm số \(y = f(x)\) và đường thẳng nằm ngang \(y = 1.5\).
2. Quan sát đồ thị:
Kẻ một đường thẳng nằm ngang đi qua tung độ \(y = 1.5\) (vị trí này nằm giữa \(y = 1\) và \(y = 2\)).
Đường thẳng này cắt đồ thị tại 3 điểm.
Tuy nhiên, đề bài hỏi số nghiệm dương (tức là xét các giao điểm có hoành độ \(x > 0\)).
3. Xác định dấu của nghiệm:
Giao điểm thứ nhất: Nằm bên trái trục tung (\(x < 0\)) \( \to \) Loại.
Giao điểm thứ hai: Nằm giữa \(x = 0\) và \(x = 2\) (\(x > 0\)) \( \to \) Nhận.
Giao điểm thứ ba: Nằm bên phải \(x = 2\) (\(x > 0\)) \( \to \) Nhận.
Vậy có 2 nghiệm dương.Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Chọn A
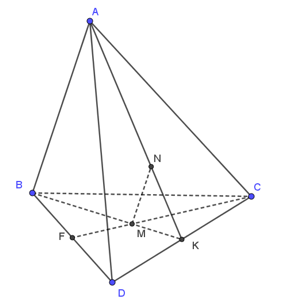
Gọi K là trung điểm của cạnh CD.
Vì M là trọng tâm tam giác BCD, nên M phải nằm trên đường trung tuyến BK.
Theo tính chất trọng tâm: \(\frac{{BM}}{{BK}} = \frac{2}{3}\) và \(\frac{{MK}}{{BK}} = \frac{1}{3}\).
Xét mặt phẳng (ABK):
Đường thẳng qua M song song với AB nằm trong mặt phẳng (ABK).
Mặt phẳng (ABK) cắt mặt phẳng (ACD) theo giao tuyến là đường thẳng AK.
Do đó, điểm N (giao điểm của đường thẳng qua M song song AB với (ACD)) phải nằm trên cạnh AK.
Áp dụng định lý Ta-lét:
Trong tam giác ABK, ta có \(MN\parallel AB\).
Theo định lý Ta-lét:
\(\frac{{MN}}{{AB}} = \frac{{KM}}{{KB}}\)
Như đã tính ở trên, \(\frac{{KM}}{{KB}} = \frac{1}{3}\).
Vậy \(\frac{{MN}}{{AB}} = \frac{1}{3}\).
Lời giải
Đáp án: 4
Giả sử nguyên liệu được giao sau mỗi $x$ ngày ($x>0$). Để đảm bảo đủ nguyên liệu cho mỗi chu kì sản xuất, doanh nghiệp phải cung cấp $5x$ đơn vị nguyên liệu gỗ cho mỗi lần vận chuyển.
Trong mỗi ngày của chu kì sản xuất, lượng nguyên liệu cần được lưu trữ trung bình là $\frac{5x}{2}$ đơn vị nguyên liệu.
Do đó, chi phí để lưu trữ nguyên liệu trong $x$ ngày của chu kì sản xuất là $200.\frac{5x}{2}.x=500{{x}^{2}}\,$ ngàn đồng.
Từ đây, chi phí cần bỏ ra cho mỗi chu kì sản xuất là $C(x)=8000+500{{x}^{2}}$ ngàn đồng.
Do đó, ta có hàm chi phí trung bình hàng ngày một chu kì sản xuất là
$c(x)=\frac{C(x)}{x}=\frac{8000+500{{x}^{2}}}{x}=\frac{8000}{x}+500x$.
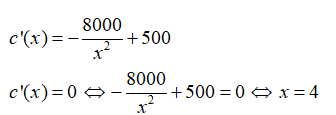
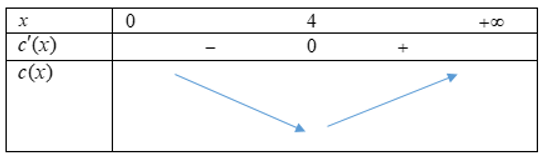
Vậy để chi phí trung bình hàng ngày trong một chu kì sản xuất là ít nhất thì doanh nghiệp nên đặt giao nguyên liệu sau 4 ngày.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.