Cho mẫu số liệu ghép nhóm có bảng tần số như sau

Tính số trung vị của mẫu số liệu trên (làm tròn đến hàng phần mười).
Quảng cáo
Trả lời:
Chọn A.
Ta có: \(n = 4 + 6 + 8 + 18 + 4 = 40\).
Nên trung vị nằm ở vị trí thứ \(20,21\) thuộc nhóm \(\left[ {31;36} \right)\).
Khi đó: \({m_e} = 31 + \frac{{20 - 4 - 6 - 8}}{{18}}.5 = 31,6\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Chọn A
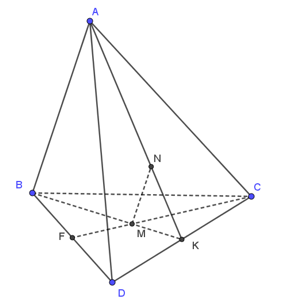
Gọi K là trung điểm của cạnh CD.
Vì M là trọng tâm tam giác BCD, nên M phải nằm trên đường trung tuyến BK.
Theo tính chất trọng tâm: \(\frac{{BM}}{{BK}} = \frac{2}{3}\) và \(\frac{{MK}}{{BK}} = \frac{1}{3}\).
Xét mặt phẳng (ABK):
Đường thẳng qua M song song với AB nằm trong mặt phẳng (ABK).
Mặt phẳng (ABK) cắt mặt phẳng (ACD) theo giao tuyến là đường thẳng AK.
Do đó, điểm N (giao điểm của đường thẳng qua M song song AB với (ACD)) phải nằm trên cạnh AK.
Áp dụng định lý Ta-lét:
Trong tam giác ABK, ta có \(MN\parallel AB\).
Theo định lý Ta-lét:
\(\frac{{MN}}{{AB}} = \frac{{KM}}{{KB}}\)
Như đã tính ở trên, \(\frac{{KM}}{{KB}} = \frac{1}{3}\).
Vậy \(\frac{{MN}}{{AB}} = \frac{1}{3}\).
Lời giải
Đáp án: 4
Giả sử nguyên liệu được giao sau mỗi $x$ ngày ($x>0$). Để đảm bảo đủ nguyên liệu cho mỗi chu kì sản xuất, doanh nghiệp phải cung cấp $5x$ đơn vị nguyên liệu gỗ cho mỗi lần vận chuyển.
Trong mỗi ngày của chu kì sản xuất, lượng nguyên liệu cần được lưu trữ trung bình là $\frac{5x}{2}$ đơn vị nguyên liệu.
Do đó, chi phí để lưu trữ nguyên liệu trong $x$ ngày của chu kì sản xuất là $200.\frac{5x}{2}.x=500{{x}^{2}}\,$ ngàn đồng.
Từ đây, chi phí cần bỏ ra cho mỗi chu kì sản xuất là $C(x)=8000+500{{x}^{2}}$ ngàn đồng.
Do đó, ta có hàm chi phí trung bình hàng ngày một chu kì sản xuất là
$c(x)=\frac{C(x)}{x}=\frac{8000+500{{x}^{2}}}{x}=\frac{8000}{x}+500x$.
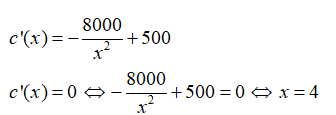
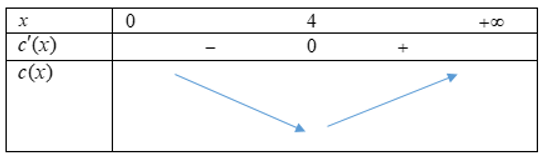
Vậy để chi phí trung bình hàng ngày trong một chu kì sản xuất là ít nhất thì doanh nghiệp nên đặt giao nguyên liệu sau 4 ngày.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.