Câu hỏi:
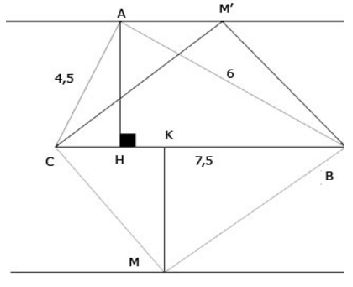
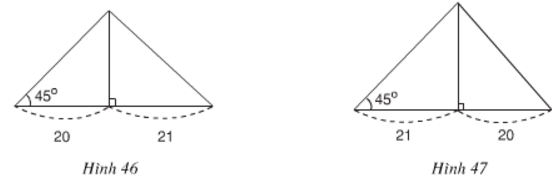
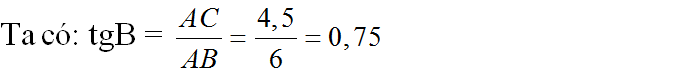13/07/2024 13,428Cho tam giác ABC có AB = 6cm, AC = 4,5cm, BC = 7,5cm.
Chứng minh tam giác ABC vuông tại A. Tính các góc B, C và đường cao AH của tam giác đó.
Câu hỏi trong đề: Giải Toán 9 phần Hình học Tập 1 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có: AB2 + AC2 = 62 + 4,52 = 7,52 = BC2
nên tam giác ABC vuông tại A. (đpcm)
=> ∠B = 37o
=> ∠C = 90o - ∠B = 90o - 37o = 53o
Mặt khác trong tam giác ABC vuông tại A, ta có:
=> AH = 3,6 cm
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
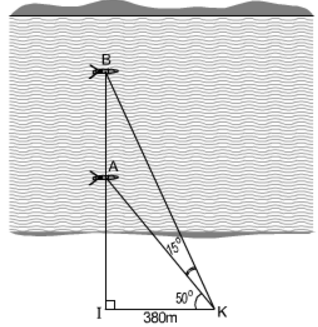
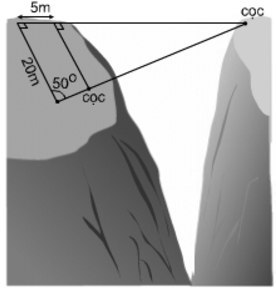
Trong tam giác vuông BIK có:
IB = IK.tg ∠IKB = IK.tg(50o + 15o) = 380.tg 65o ≈ 814 (m)
Trong tam giác vuông AIK có:
IA = IK.tg ∠IKA = IK.tg 50o = 380.tg50o ≈ 452 (m)
Vậy khoảng cách giữa hai thuyền là:
AB = IB – IA = 814 – 452 = 362 (m)
Lời giải
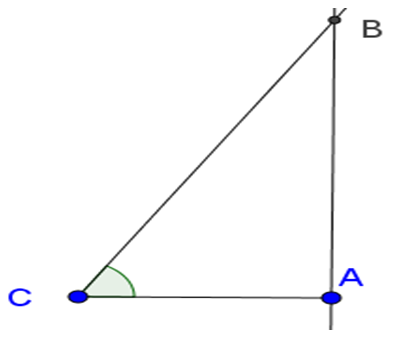
Kí hiệu như hình vẽ.
Trong tam giác vuông ABC có:
AC = BC.cosC = 3.cosC
Vì phải đặt thang tạo với mặt đất một góc 60o đến 70o nên
60o ≤ ∠C ≤ 70o
=> cos 70o ≤ cosC ≤ cos 60o
=> 3.cos 70o ≤ 3.cosC ≤ 3.cos 60o
=> 1,03 ≤ AC ≤ 1,5
Vậy phải đặt chân thang cách tường từ 1,03 m đến 1,5 m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
-
Chuyên đề 8: Hình học (có đáp án)