Câu hỏi:
13/07/2024 26,219Ở một cái thang dài 3m người ta ghi: "Để đảm bảo an toàn khi dùng thang, phải đặt thang này tạo với mặt đất một góc có độ lớn từ 60o đến 70o". Đo góc thì khó hơn đo độ dài. Vậy hãy cho biết: Khi dùng thang đó chân thang phải đặt cách tường khoảng bao nhiêu mét để đảm bảo an toàn?
Câu hỏi trong đề: Giải Toán 9 phần Hình học Tập 1 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Kí hiệu như hình vẽ.
Trong tam giác vuông ABC có:
AC = BC.cosC = 3.cosC
Vì phải đặt thang tạo với mặt đất một góc 60o đến 70o nên
60o ≤ ∠C ≤ 70o
=> cos 70o ≤ cosC ≤ cos 60o
=> 3.cos 70o ≤ 3.cosC ≤ 3.cos 60o
=> 1,03 ≤ AC ≤ 1,5
Vậy phải đặt chân thang cách tường từ 1,03 m đến 1,5 m.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
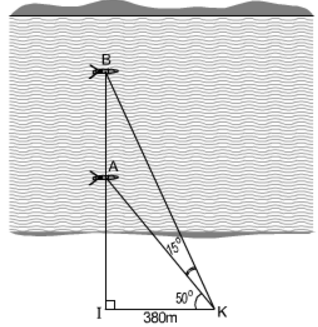
Trong tam giác vuông BIK có:
IB = IK.tg ∠IKB = IK.tg(50o + 15o) = 380.tg 65o ≈ 814 (m)
Trong tam giác vuông AIK có:
IA = IK.tg ∠IKA = IK.tg 50o = 380.tg50o ≈ 452 (m)
Vậy khoảng cách giữa hai thuyền là:
AB = IB – IA = 814 – 452 = 362 (m)
Lời giải
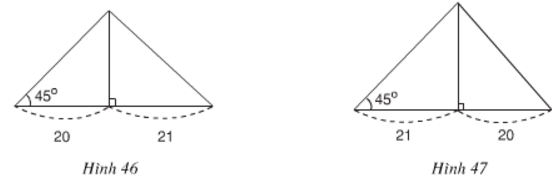
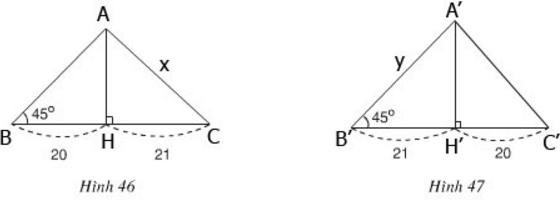
- Trường hợp hình 46: cạnh lớn trong hai cạnh còn lại được kí hiệu là x.
ΔHAB cân vì có ∠B = 45o
=> HA = HB = 20
Áp dụng định lí Pitago trong ΔHAC có:
x2 = AC2 = HA2 + HC2 = 202 + 212 = 841
=> x = 29 hay độ dài cạnh lớn trong hai cạnh còn lại là 29.
QUẢNG CÁO
- Trường hợp hình 47: cạnh lớn trong hai cạnh còn lại được kí hiệu là y.
ΔH'A'B' cân vì có ∠B' = 45o
=> H'A' = H'B' = 21
Áp dụng định lí Pitago trong ΔH'A'B' có:
y2 = A'B'2 = H'A'2 + H'B'2 = 212 + 212 = 2.212
=> y = 21√2 ≈ 29,7 hay độ dài cạnh lớn trong hai cạnh còn lại là 29,7.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
-
Chuyên đề 8: Hình học (có đáp án)