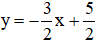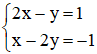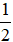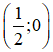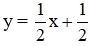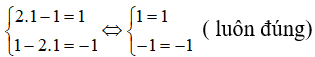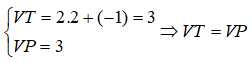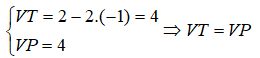Cho hai phương trình 2x + y = 4 và 3x + 2y = 5.
Tìm nghiệm tổng quát của mỗi phương trình trên
Câu hỏi trong đề: Toán 9 Tập 2 - phần Đại số !!
Quảng cáo
Trả lời:
+ Xét phương trình 2x + y = 4 (1) ⇔ y = -2x + 4
Vậy phương trình (1) có nghiệm tổng quát là (x ; -2x + 4) (x ∈ R).
+ Xét phương trình 3x + 2y = 5 (2) ⇔
Vậy phương trình (2) có nghiệm tổng quát là : 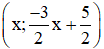
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Xét hệ (I):
Ta biểu diễn hai đường thẳng (d): 2x – y = 1 và (d’): x – 2y = -1 trên mặt phẳng tọa độ.
+ Xét đường thẳng (d): 2x – y = 1 hay (d) : y = 2x – 1
Chọn x = 0 ⇒ y = -1.
Chọn y = 0 ⇒ x =
⇒ (d) đi qua hai điểm (0; -1) và
+ Xét (d’) : x – 2y = -1 hay (d’):
Chọn x = 0 ⇒ y =
Chọn y = 0 ⇒ x = -1.
⇒ (d’) đi qua hai điểm 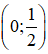
Dựa vào đồ thị thấy hai đường thẳng (d) và (d’) cắt nhau tại A (1; 1).
Thử lại, thay x =1, y=1 vào các phương trình của hệ (I) ta được:
Vậy hệ phương trình (I) có một nghiệm là (1; 1)
Lời giải
Thay x = 2 , y = -1 vào phương trình 2x + y = 3 ta được:
Vậy (2;-1) là nghiệm của phương trình 2x+y=3
- Thay x = 2, y = -1 vào phương trình x – 2y = 4 ta được:
Vậy (2;-1) là nghiệm của phương trình x – 2y = 4
Vậy cặp số (x; y) = (2; -1) vừa là nghiệm của phương trình thứ nhất, vừa là nghiệm của phương trình thứ hai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.