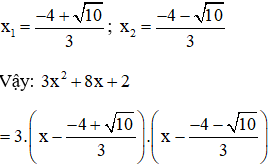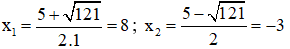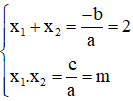Chứng tỏ rằng nếu phương trình ax2 + bx + c = 0 có nghiệm là x1 và x2 thì tam thức ax2 + bx + c phân tích được thành nhân tử như sau:
ax2 + bx + c = a( x - x1)(x - x2)
Áp dụng : phân tích đa thức thành nhân tử.
3x2 + 8x + 2
Câu hỏi trong đề: Toán 9 Tập 2 - phần Đại số !!
Quảng cáo
Trả lời:
3x2 + 8x + 2 = 0
Có a = 3; b' = 4; c = 2
⇒ Δ’ = 42 – 2.3 = 10 > 0
⇒ Phương trình có hai nghiệm phân biệt:
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
u – v = 5 ⇒ u + (-v) = 5
u.v = 24 ⇒ u.(-v) = -uv = -24.
Ta tìm u và –v. Từ đó, ta dễ dàng tính được u và v.
S= u + (-v) = 5; P = u. (-v) = -24 ⇒ S2 – 4P = 52 – 4.(-24) = 121 > 0
⇒ u và –v là hai nghiệm của phương trình: x2 – 5x – 24 = 0
Có Δ = (-5)2 – 4.1.(-24) = 121
⇒ Phương trình có hai nghiệm phân biệt
⇒ u = 8; -v = -3 hoặc u = -3; -v = 8
⇒ u = 8; v = 3 hoặc u = -3; v = -8.
Lời giải
Phương trình x2 – 2x + m = 0
Có a = 1; b = -2; c = m nên b’= -1
⇒ Δ’ = (-1)2 – 1.m = 1 – m
Phương trình có nghiệm ⇔ Δ’ ≥ 0 ⇔ 1 – m ≥ 0 ⇔ m ≤ 1.
Khi đó, theo định lý Vi-et:
Vậy với m ≤ 1, phương trình có hai nghiệm có tổng bằng 2; tích bằng m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.