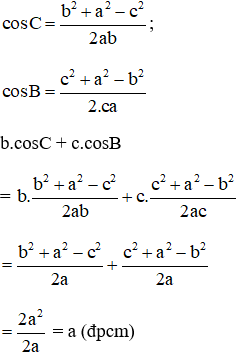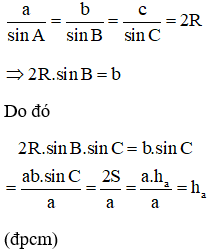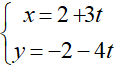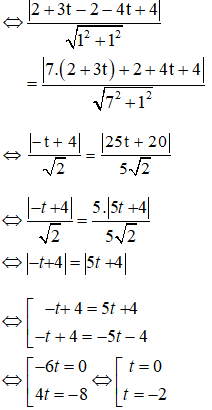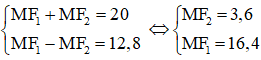Câu hỏi:
31/03/2020 48,622Chứng minh rằng trong mọi tam giác ABC ta đều có:
a, a = b cosC + c cosB;
b, sinA = sinBcosC + sinCcosB;
c, ha = 2RsinBsinC.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Áp dụng hệ quả của định lí côsin trong tam giác ta có:
b) Theo định lí tổng ba góc của tam giác ta có:
A + B + C = 180º
⇒ sin A = sin [180º – (B – C)]= sin (B + C) = sinB.cos C + cosB. sinC (đpcm)
c) Theo định lí sin trong tam giác ABC, ta có:
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Giả sử đường tròn cần lập có tâm O; bán kính R.
Đường thẳng Δ đi qua M(2; -2) và có VTPT là n→(4; 3) nên đường thẳng này có 1 VTCP là u→(3; -4) . Phương trình tham số của đường thẳng Δ là:
O nằm trên Δ ⇒ O(2 + 3t; -2 – 4t)
Đường tròn (O; R) tiếp xúc với d1 và d2 ⇒ d(O; d1) = d(O; d2) = R
Ta có: d(O; d1) = d(O; d2)
+ Với t = 0 ⇒ O(2; -2) ⇒ R = d(O; d1) = 2√2
Phương trình đường tròn: (x – 2)2 + (y + 2)2 = 8.
+ Với t = -2 ⇒ O(-4; 6) , R = d(O; d1) = 3√2
Phương trình đường tròn: (x + 4)2 + (y – 6)2 = 18
Vậy có hai phương trình đường tròn thỏa mãn là:
(x – 2)2 + (y + 2)2 = 8 hoặc (x + 4)2 + (y – 6)2 = 18
Lời giải
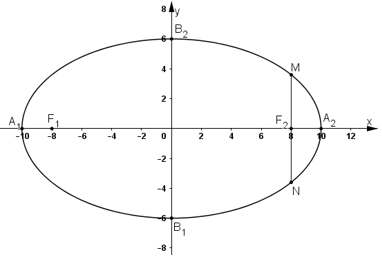
a) (E):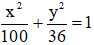 
có a = 10; b = 6 ⇒ c2 = a2 – b2 = 64 ⇒ c = 8.
+ Tọa độ các đỉnh của elip là: A1(-10; 0); A2(10; 0); B1(0; -6); B2(0; 6)
+ Tọa độ hai tiêu điểm của elip: F1(-8; 0) và F2(8; 0)
+ Vẽ elip:
b) Ta có: M ∈ (E) ⇒ MF1 + MF2 = 2a = 20 (1)
MN // Oy ⇒ MN ⊥ F1F2 ⇒ MF12 – MF22 = F1F22 = (2c)2 = 162
⇒ (MF1 + MF2).(MF1 – MF2) = 162
⇒ MF1 – MF2 = 12,8 (Vì MF1 + MF2 = 20) (2).
Từ (1) và (2) ta có hệ phương trình
Vậy MN = 2.MF2 = 7,2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
13 câu Trắc nghiệm Tích của vectơ với một số có đáp án (Thông hiểu)
-
12 Bài tập Ứng dụng của hàm số bậc hai để giải bài toán thực tế (có lời giải)
-
16 câu Trắc nghiệm Toán 10 Kết nối tri thức Mệnh đề có đáp án
-
10 Bài tập Ứng dụng ba đường conic vào các bài toán thực tế (có lời giải)
-
10 Bài tập Tìm hệ số, số hạng trong khai triển nhị thức Newton (có lời giải)
-
10 Bài tập Cách xét tính đúng sai của mệnh đề (có lời giải)
-
10 Bài tập Cách xét tính đúng sai của mệnh đề (có lời giải)
-
10 Bài tập Tính số trung bình, trung vị, tứ phân vị và mốt của mẫu số liệu cho trước (có lời giải)
Nhắn tin Zalo