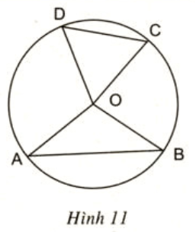
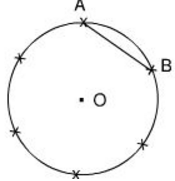
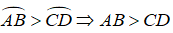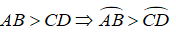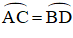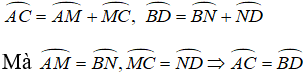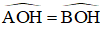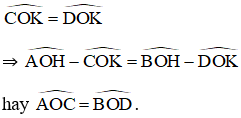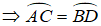Xem hình 11.
Hãy viết giả thiết và kết luận của định lý
(Không yêu cầu học sinh chứng minh định lý này)
Câu hỏi trong đề: Giải Toán 9 phần Hình học Tập 2 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Vẽ đường tròn tâm O, các dây cung AB // CD.
Cần chứng minh 
Cách 1:
Kẻ bán kính MN // AB // CD
MN // AB
+ TH1: AB và CD cùng nằm trong một nửa đường tròn.
.
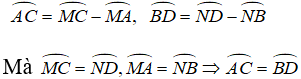
+ TH2: AB và CD thuộc hai nửa đường tròn khác nhau.
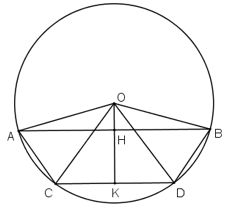
Cách 2:
Kẻ OH ⊥ AB; OK ⊥ CD (H ∈ AB, K ∈ CD)
Vì AB // CD ⇒ O, H, K thẳng hàng.
ΔOAB có OA = OB
⇒ ΔOAB cân tại O
⇒ đường cao OH đồng thời là đường phân giác
⇒ 
Chứng minh tương tự:
Lời giải
+) Cho đường tròn (O); dây cung AB; I là điểm chính giữa cung , H = OI ∩ AB
Ta có:
Suy ra: sđ = sđ
Do đó:
Xét ΔAOH và ΔBOH có:
AO = OB,
OH chung
Suy ra ΔAOH = ΔBOH (c – g – c)
Do đó
Mà là hai góc kề bù nên
OH ⊥ AB.
Vậy đường kính đi qua điểm chính giữa của cung thì vuông góc với dây căng cung ấy.
+) Cho đường tròn (O); dây cung AB.
Kẻ đường thẳng OH ⊥ AB (H ∈ AB) cắt đường tròn tại I.
Ta có: ΔABO cân tại O (vì AO = OB = R).
Đường cao OH đồng thời là đường phân giác
Suy ra
Hay
Suy ra
I là điểm chính giữa của cung
Vậy đường kính vuông góc với dây căng cung thì đi qua điểm chính giữa của cung.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo