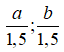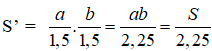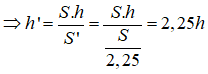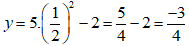Câu hỏi:
18/04/2020 824Ông B dự định xây một bể nước có thể tích V, nhưng sau đó ông muốn thay đổi kích thước so với dự định ban đầu như sau: giảm cả chiều dài và chiều rộng đáy bể 1,5 lần. Hỏi chiều cao của bể phải thay đổi như thế nào để bể xây được vẫn có thể tích là V?
Câu hỏi trong đề: Sách bài tập Toán 7 Tập 1 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
* Thể tích hình hộp chữ nhật V = S.h
Trong đó; S là diện tích đáy và h là chiều cao của hình hộp chữ nhật.
* Gọi chiều dài, chiều rộng và chiều cao của bể nước theo dự định ban đầu lần lượt là a, b và h (a, b, h > 0).
Khi giảm cả chiều dài và chiều rộng đáy bể đi 1,5 lần ta được chiều dài và chiều rộng mới là: 
* Diện tích đáy bể theo dự định ban đầu là: S = ab.
Diện tích đáy bể sau khi thay đổi kích thước là: 
* Vì thể tích không đổi nên diện tích đáy bể và chiều cao là hai đaị lượng tỉ lệ nghịch nên ta có: S.h = S’.h’
Vậy để thể tích bể không đổi thì chiều cao bể tăng gấp 2,25 lần so với dự định
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Tại x = 1/2 ta có: 
Vậy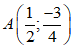 
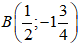
thuộc đồ thị hàm số
không thuộc đồ thị hàm số.
Tại x = 2 thì y = 5.22 – 2 = 18.
Vậy điểm C(2; 18) thuộc đồ thị hàm số.
Lời giải
Gọi thể tích thanh nhôm là x (cm3), thanh sắt là y (cm3)
Vì khối lượng hai thanh bằng nhau nên thể tích tỉ lệ nghịch với khối lượng riêng.
Ta có: x/y = 7,8/2,7 ≈ 2,9
Vậy thể tích thanh nhôm lớn hơn thể tích thanh sắt khoảng 2,9 lần
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
-
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 01
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
-
Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 02
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 02
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận