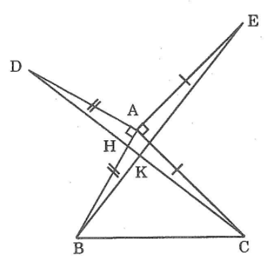
Cho tam giác ABC có ba góc nhọn. Vẽ đoạn thẳng AD vuông góc với AB và bằng AB (D khác phía C đối với AB), vẽ đoạn thẳng AE vuông góc với AC và bằng AC (E khác phía B đối với AC).Chứng minh rằng: DC ⊥BE
Câu hỏi trong đề: Sách bài tập Toán 7 Tập 1 !!
Quảng cáo
Trả lời:
Gọi giao điểm DC và AB là H, giao điểm của CD và BE là K
Ta có: ΔABE = ΔADC (cmt)
⇒ ∠ABE = ∠ADC (hai góc t.ư)
hay ∠HBK = ∠ADH
+ ΔADH và ΔBKH đều có tổng ba góc trong mỗi tam giác bằng 180o nên có:
∠ADH + ∠DAH + ∠AHD = ∠BKH + ∠KHB + ∠HBK
Mà ∠AHD = ∠BHK (hai góc đối đỉnh)
∠ADH = ∠HBK (chứng minh trên)
Suy ra ∠DAH = ∠HKB
Mà ∠DAH = 90o nên ∠HKB = 90o
⇒ DC ⊥ BE (điều phải chứng minh)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 8 (chương trình mới) ( 120.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Xét Δ AOC và Δ BOD, ta có:
OA = OB ( Vì O là trung điểm của AB )
∠(AOC) =∠(BOD) (đối đỉnh)
OC = OD ( Vì O là trung điểm của CD)
Suy ra: ΔAOC = ΔBOD (c.g.c)
⇒∠A =∠B (hai góc tương ứng)
Vậy: AC // BD (vì có hai góc so le trong bằng nhau)
Lời giải
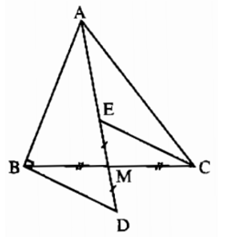
+) Xét ΔBMD và ΔCME có:
BM = MC (vì M là trung điểm BC)
MD = ME (giả thiết)
∠BMD = ∠EMC (hai góc đối đỉnh)
⇒ ΔBMD = ΔCME (c.g.c)
⇒ ∠D = ∠MEC (hai góc t.ư)
Mà hai góc này ở vị trí so le trong nên suy ra BD // CE.
Ta có AB ⊥ BD (giả thiết) và BD // CE (chứng minh trên) nên AB ⊥ CE
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Hữu Trí Đỗ
sai that
Liên Nguyễn
Thật ko vậy để tớ đi check
tường anh nguyễn
giải sai r ạ