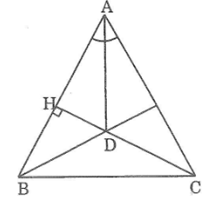
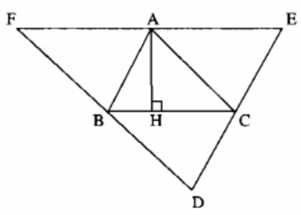
Cho tam giác ABC cân tại A, đường cao CH cắt tia phân giác của góc A tại D. Chứng minh rằng BD vuông góc với AC.
Câu hỏi trong đề: Sách bài tập Toán 7 Tập 2 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Vì ΔABC cân tại A nên đường phân giác của góc ở đỉnh A cũng là đường cao từ A.
Suy ra: AD ⊥ BC
Ta có: CH ⊥ AB (gt)
Tam giác ABC có hai đường cao AD và CH cắt nhau tại D nên D là trực tâm của ∆ABC
Suy ra BD là đường cao xuất phát từ đỉnh B đến cạnh AC.
Vậy BD ⊥ AC.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
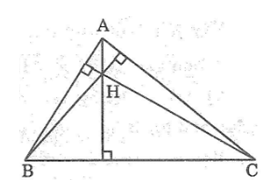
Trong ΔABC ta có H là trực tâm nên:
AH ⊥ BC, BH ⊥ AC, CH ⊥ AB
Trong ΔAHB, ta có:
AC ⊥ BH
BC ⊥ AH
Vì hai đường cao kẻ từ A và B cắt nhau tại C nên C là trực tâm của tam giác AHB.
Trong ΔHAC, ta có:
AB ⊥ CH
CB ⊥ AH
Vì hai đường cao kẻ từ A và C cắt nhau tại B nên B là trực tâm của ΔHAC.
Trong ΔHBC, ta có:
BA ⊥ HC
CA ⊥ BH
Vì hai đường cao kẻ từ B và C cắt nhau tại A nên A là trực tâm của tam giác HBC.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
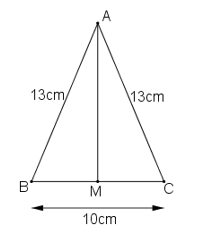
Tam giác ABC có AB = AC = 13 cm nên tam giác ABC cân tại A
Suy ra: đường trung tuyến AM cũng là đường cao.
Suy ra: AM ⊥ BC
Ta có: MB = MC = 1/2 BC = 1/2 .10 = 5 (cm)
Trong tam giác vuông AMB có ∠(AMB) = 90o
Áp dụng định lý Pitago ta có:
AB2 = AM2 + MB2
Suy ra: AM2 = AB2 - MB2
= 132 - 52 = 169 - 25 = 144
Vậy AM = 12(cm)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập