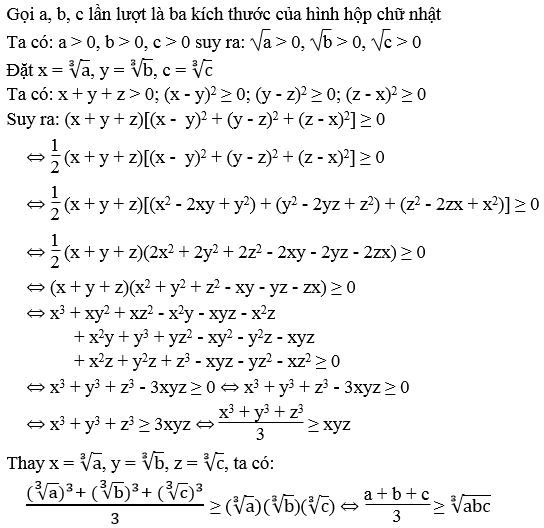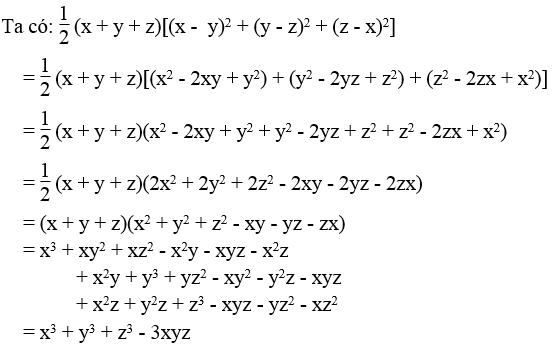Câu hỏi:

13/07/2024 990

Áp dụng bất đẳng thức Cô-si cho ba số không âm, chứng minh: Trong các hình hộp chữ nhật có cùng tổng ba kích thước thì hình lập phương có thể tích lớn nhất.

Xem lời giải

Câu hỏi trong đề: Giải Sách Bài Tập Toán 9 Tập 1 !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Giải sách bài tập Toán 9 | Giải bài tập Sách bài tập Toán 9

Các hình hộp chữ nhật có cùng tổng ba kích thước thì $\frac{a + b + c}{3}$ không đổi.

Vì $\frac{a + b + c}{3}$ $\geq$ $\sqrt[3]{a b c}$ và $\frac{a + b + c}{3}$ không đổi nên $\sqrt[3]{a b c}$ đạt giá trị lớn nhất $\frac{a + b + c}{3}$ khi a = b = c.

Vậy trong các hình hộp chữ nhật có cùng tổng ba kích thước thì hình lập phương có thể tích lớn nhất.

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Chứng minh: $x^{3} + y^{3} + z^{3} - 3 x y z = 1 / 2 . (x + y + z) [{(x - y)}^{2} + {(y - z)}^{2} + {(z - x)}^{2}]$
Từ đó chứng tỏ: Với ba số x, y, z không âm thì $\frac{x^{3} + y^{3} + z^{3}}{3} \geq x y z$

Xem đáp án

Lời giải

Giải sách bài tập Toán 9 | Giải bài tập Sách bài tập Toán 9

Vế trái bằng vế phải nên đẳng thức được chứng minh.

Nếu x $\geq$ 0, y $\geq$ 0, z $\geq$ 0 thì:

x + y + z $\geq$ 0

${(x - y)}^{2} + {(y - z)}^{2} + {(z - x)}^{2} \geq 0$

Suy ra:

$x^{3} + y^{3} + z^{3} - 3 x y z \geq 0 \Leftrightarrow x^{3} + y^{3} + z^{3} \geq 3 x y z$

Hay: $\frac{x^{3} + y^{3} + z^{3}}{3} \geq x y z$

Câu 2

Tính (không dùng bảng tính hay máy tính bỏ túi):
$\sqrt[3]{- 343}; \sqrt[3]{0, 027}; \sqrt[3]{1, 331}; \sqrt[3]{- 0, 521}$

Xem đáp án

Lời giải

Giải sách bài tập Toán 9 | Giải bài tập Sách bài tập Toán 9

Câu 3

Tìm x, biết: $\sqrt[3]{x - 5} = 0, 9$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Tìm giá trị gần đúng của căn bậc ba mỗi số sau bằng bảng lập phương và kiểm tra bằng máy tính bỏ túi (làm tròn đến chữ số thập phân thứ ba): 12

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Tìm x, biết: $\sqrt[3]{x} = - 1, 5$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Chứng minh các bất đẳng thức sau: $\sqrt[3]{a^{3} b} = a \sqrt[3]{b}$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Áp dụng bất đẳng thức Cô-si cho ba số không âm, chứng minh: Trong các hình hộp chữ nhật có cùng tổng ba kích thước thì hình lập phương có thể tích lớn nhất.

Bình luận

Chứng minh: x3+y3+z3-3xyz=1/2.x+y+zx-y2+y-z2+z-x2Từ đó chứng tỏ: Với ba số x, y, z không âm thì x3+y3+z33≥xyz

Tính (không dùng bảng tính hay máy tính bỏ túi):-3433; 0,0273; 1,3313; -0,5213

Tìm x, biết: x-53=0,9

Tìm giá trị gần đúng của căn bậc ba mỗi số sau bằng bảng lập phương và kiểm tra bằng máy tính bỏ túi (làm tròn đến chữ số thập phân thứ ba): 12

Tìm x, biết: x3=-1,5

Chứng minh các bất đẳng thức sau: a3b3=ab3

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Chứng minh: $x^{3} + y^{3} + z^{3} - 3 x y z = 1 / 2 . (x + y + z) [{(x - y)}^{2} + {(y - z)}^{2} + {(z - x)}^{2}]$
Từ đó chứng tỏ: Với ba số x, y, z không âm thì $\frac{x^{3} + y^{3} + z^{3}}{3} \geq x y z$

Tính (không dùng bảng tính hay máy tính bỏ túi):
$\sqrt[3]{- 343}; \sqrt[3]{0, 027}; \sqrt[3]{1, 331}; \sqrt[3]{- 0, 521}$

Tìm x, biết: $\sqrt[3]{x - 5} = 0, 9$

Tìm x, biết: $\sqrt[3]{x} = - 1, 5$

Chứng minh các bất đẳng thức sau: $\sqrt[3]{a^{3} b} = a \sqrt[3]{b}$