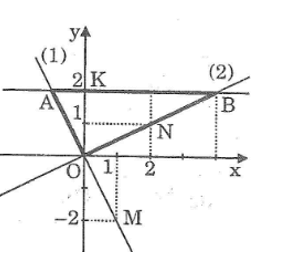
Đường thẳng (d) song song với trục Ox và cắt trục tung Oy tại điểm C có tung độ bằng 2, theo thứ tự cắt các đường thẳng (1) và (2) tại D và E. Tìm tọa độ của các điểm D, E. Tính chu vi và diện tích tam giác ODE.
Câu hỏi trong đề: Giải Sách Bài Tập Toán 9 Tập 1 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Qua điểm C trên trục tung có tung độ bằng 2, kẻ đường thẳng song song với Ox cắt đồ thị hàm số y = x tại D, cắt đồ thị hàm số y = 0,5x tại E.
Điểm D có tung độ bằng 2.
Thay giá trị y = 2 vào hàm số y = x ta được x = 2.
Vậy điểm D(2; 2)
Điểm E có tung độ bằng 2.
Thay giá trị y = 2 vào hàm số y = 0,5x ta được x = 4
Vậy điểm E(4; 2)
Gọi D’ và E’ lần lượt là hình chiếu của D và E trên Ox.
Ta có: OD’ = 2, OE’ = 4
Áp dụng định lí Pi-ta-go vào tam giác vuông ODD’, ta có:
Suy ra: OD =
Áp dụng định lí Pi-ta-go vào tam giác vuông OEE’, ta có:
20
Suy ra: OE =
Lại có: DE = CE – CD = 4 – 2 = 2
Chu vi tam giác ODE bằng: OD + DE + EO =
= 2
Diện tích tam giác ODE bằng: 1/2.DE.OC = 1/2.2.2 = 2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi cuối kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đường thẳng đi qua gốc tọa độ có dạng y = ax + b
Vì đường thẳng y = ax đi qua điểm A(2; 1) nên tọa độ điểm A nghiệm đúng phương trình đường thẳng.
Ta có: 1 = a.2 ⇔ a = 1/2
Vậy hệ số góc của đường thẳng đi qua gốc tọa độ và đi qua điểm A(2; 1) là a = 1/2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chọn C
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập