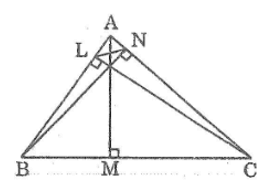
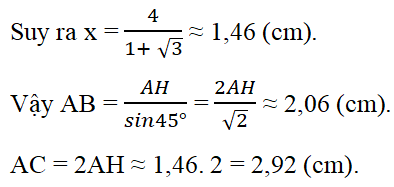Gọi AM, BN, CL lần lượt là ba đường cao của tam giác ABC. Chứng minh: AN.BL.CM = AB.BC.CA.cosA.cosB.cosC
Câu hỏi trong đề: Giải Sách Bài Tập Toán 9 Tập 1 !!
Quảng cáo
Trả lời:
ABN vuông tại N nên AN = AB.cosB (1)
BCL vuông tại L nên BL = BC.cosB (2)
ACM vuông tại M nên CM = AC.cosC (3)
Từ (1), (2) và (3) suy ra: AN.BL.CM = AB.BC.CA. cosA cosB cosC
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
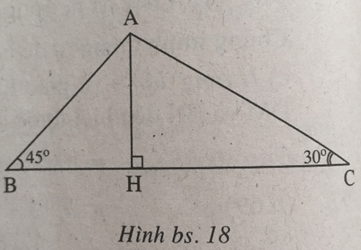
Vẽ đường cao AH. Đặt BH = x, CH = y thì do H nằm giữa B và C (hai góc B, C là góc nhọn) suy ra x + y = 4 (xem h.bs.18).
Ta có BH = AH = HC.tg nên x – y.tg = y/
AC = 2AH ≈ 1,46. 2 = 2,92 (cm).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.