Câu hỏi:
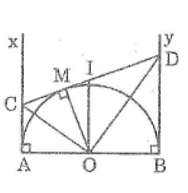
11/07/2024 4,343, By (Ax, By và nửa đường tròn thuộc cùng một mặt phẳng bờ AB). Gọi M là một điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại M cắt Ax, By theo thứ tự ở C và D. Tìm vị trí của điểm M để hình thang ABDC có chu vi nhỏ nhất
Câu hỏi trong đề: Giải Sách Bài Tập Toán 9 Tập 1 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Theo tính chất hai tiếp tuyến cắt nhau ta có:
CA = CM
DB = DM
Suy ra: AC + BD = CM + DM = CD
Chu vi hình thang ABDC bằng: AB + BD + DC + CA = AB + 2CD
Vì đường kính AB của (O) không thay đổi nên chu vi hình thang nhỏ nhất khi CD nhỏ nhất
Ta có: CD AB nên CD nhỏ nhât khi và chỉ khi CD = AB
Khi đó CD // AB ⇔ OM ⊥ AB
Vậy khi M là giao điểm của đường thẳng vuông góc với AB tại O với nửa đường tròn (O) thì hình thang ABDC có chu vi nhỏ nhất.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
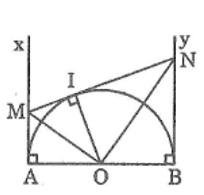
Gọi I là tiếp điểm của tiếp tuyến MN với đường tròn (O). Nối OI
Ta có: 
(hai góc kề bù)
OM là tia phân giác của góc AOI (tính chất hai tiếp tuyến cắt nhau)
ON là tia phân giác của góc BOI (tính chất hai tiếp tuyến cắt nhau)
Suy ra : OM ⊥ ON (tính chất hai góc kề bù)
Vậy 
Lời giải
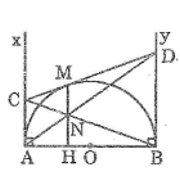
Ax ⊥ AB
By ⊥ AB
Suy ra: Ax // By hay AC // BD
Trong tam giác BND, ta có AC // BD
Suy ra: ND/NA = BD/AC (hệ quả định lí Ta-lét) (1)
Theo tính chất hai tiếp tuyến cắt nhau, ta có:
AC = CM và BD = DM (2)
Từ (1) và (2) suy ra: ND/NA = MD/MC
Trong tam giác ACD, ta có: ND/NA = MD/MC
Suy ra: MN // AC (theo định lí đảo định lí Ta-lét)
Mà: AC ⊥ AB (vì Ax ⊥ AB)
Suy ra: MN ⊥ AB
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Chuyên đề 8: Hình học (có đáp án)
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận