Bài 6: Tính chất của hai tiếp tuyến cắt nhau
58 người thi tuần này 4.6 64.3 K lượt thi 33 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
20 bài tập Toán 9 Cánh diều Bài 2. Hình nón có đáp án
Danh sách câu hỏi:
Lời giải
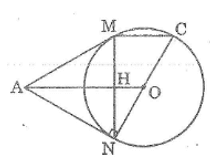
Ta có: AM = AN (tính chất hai tiếp tuyến cắt nhau)
Suy ra tam giác AMN cân tại A
Mặt khác AO là đường phân giác của góc MAN (tính chất hai tiếp tuyến cắt nhau)
Suy ra AO là đường cao của tam giác AMN (tính chất tam giác cân)
Vậy OA ⊥ MN.
Lời giải
Tam giác MNC nội tiếp trong đường tròn (O) có NC là đường kính nên góc (CMN) =
Suy ra: NM ⊥ MC
Mà OA ⊥ MN (chứng minh trên)
Suy ra: OA // MC
Lời giải
Ta có: AN ⊥ NC (tính chất tiếp tuyến)
Áp dụng định lí Pitago vào tam giác vuông AON ta có :
Suy ra : = 16
AN = 4 (cm)
Suy ra: AM = AN = 4 (cm)
Gọi H là giao điểm của AO và MN
Ta có: MH = NH = MN/2 (tính chất tam giác cân)
Tam giác AON vuông tại N có NH ⊥ AO. Theo hệ thức lượng trong tam giác vuông, ta có:
OA.NH = AN.ON ⇒ NH = (AN.ON)/AO = (4.3)/5 = 2,4 (cm)
MN = 2.NH = 2.2,4 = 4,8 (cm)
Lời giải
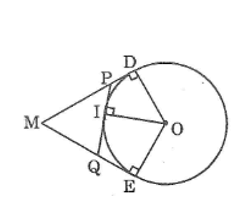
Ta có: MD = ME (tính chất hai tiếp tuyến cắt nhau)
PD = PI (tính chất hai tiếp tuyến cắt nhau)
QI = QE (tính chất hai tiếp tuyến cắt nhau)
Chu vi tam giác APQ bằng:
MP + PQ + QM
= MP + PI + IQ + QM
= MP + PD + QM + QE
= MD + ME
= 2.MD
= 2.4 = 8 (cm)
Lời giải
* Phân tích
Giả sử đường tròn (I) dựng được thỏa mãn điều kiện bài toán
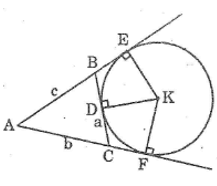
- Đường tròn (I) tiếp xúc với Ox và Oy nên điểm I nằm trên tia phân giác của góc xOy
- Đường tròn (I) tiếp xúc với Ox tại A nên I nằm trên đường vuông góc với Ox kẻ từ A
Vậy I là giao điểm của tia phân giác góc xOy và đường thẳng vuông góc với Ox tại A
* Cách dựng
- Dựng tia phân giác của góc xOy
- Dựng đường thẳng vuông góc với Ox tại A cắt tia phân giác của góc xOy tại I
- Dựng đường tròn (I; IA)
* Chứng minh
Ta có: Ox ⊥ IA tại A nên Ox là tiếp tuyến của (I)
I nằm trên tia phân giác của góc xOy nên I cách đều hai cạnh Ox, Oy. Khi đó khoảng cách từ I đến Oy bằng IA nên Oy cũng là tiếp tuyến của đường tròn (I).
Vậy đường tròn (I) đi qua A và tiếp xúc với hai cạnh của góc xOy.
* Biện luận
Vì góc xOy nhỏ hơn nên góc tạo bởi một cạnh của góc với tia phân giác là góc nhọn. Khi đó đường thẳng vuông góc với Ox tại A luôn cắt tia phân giác của góc xOy.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.