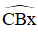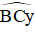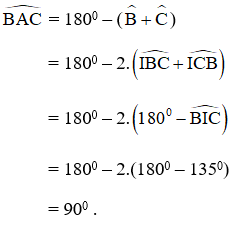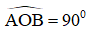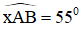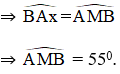Giải bài tập SGK Toán 9 tập 2 hay nhất Bài 6: Cung chứa góc
28 người thi tuần này 4.6 1.9 K lượt thi 6 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
19 bài tập Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
20 bài tập Toán 9 Cánh diều Bài 2. Hình nón có đáp án
Danh sách câu hỏi:
Lời giải
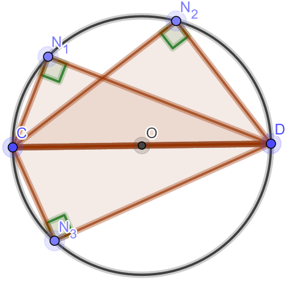
Vẽ Hình
b) Vì 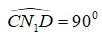
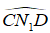
Tương tự như vậy ta chứng minh được nằm trên đường tròn đường kính CD
Vậy nằm trên đường tròn đường kính CD
Lời giải
Qũy đạo chuyển động của điểm M là hai cung tròn đối xứng nhau qua dây AB
Lời giải
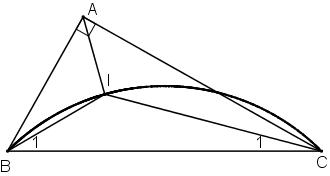
* Dự đoán : Quỹ tích điểm I là cung chứa góc dựng trên đoạn BC.
* Chứng minh :
Phần thuận : Chứng minh mọi điểm I thỏa mãn điều kiện trên đều thuộc cung chứa góc dựng trên đoạn BC.
⇒ I thuộc cung chứa góc dựng trên đoạn thẳng BC.
Phần đảo: Chứng minh mọi điểm I thuộc cung chứa góc dựng trên đoạn BC, đều có tam giác ABC thỏa mãn điều kiện.
+ Lấy I trên cung chứa góc dựng trên đoạn BC
+ Kẻ tia Bx sao cho BI là phân giác của
+ Kẻ tia Cy sao cho CI là phân giác của
+ Bx cắt Cy tại A.
Khi đó I là giao điểm của hai đường phân giác trong tam giác ABC
Vậy ΔABC vuông tại A thỏa mãn đề bài.
Kết luận : Quỹ tích điểm I là toàn bộ cung chứa góc dựng trên đoạn BC (khác B và C).
Kiến thức áp dụng
+ Thông thường, bài toán quỹ tích ta làm theo các bước :
1, Dự đoán quỹ tích
2, Chứng minh quỹ tích : gồm Phần thuận và Phần đảo
3, Kết luận.
+ Quỹ tích các điểm M thỏa mãn 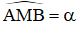
Lời giải
Dự đoán: Quỹ tích cần tìm là nửa đường tròn đường kính AB.
Chứng minh phần thuận:
ABCD là hình thoi
⇒ AC ⊥ BD ( hình thoi có 2 đường chéo vuông góc với nhau)
⇒
Vậy quỹ tích của O là nửa đường tròn đường kính AB.
Chứng minh phần đảo: Chứng minh với mọi điểm O thuộc nửa đường tròn đường kính AB ta đều có hình thoi ABCD thỏa mãn đề bài.
+ Lấy điểm O thuộc nửa đường tròn đường kính AB
+ Lấy C đối xứng với A qua O
+ Lấy D đối xứng với B qua O.
Tứ giác ABCD có AC cắt BD tại O là trung điểm mỗi đường
⇒ ABCD là hình bình hành.
Mà O thuộc nửa đường tròn đường kính AB
⇒
⇒ AC ⊥ DB
⇒ Hình bình hành ABCD là hình thoi.
Kết luận: Quỹ tích điểm O là nửa đường tròn đường kính AB (khác A và B)
Kiến thức áp dụng
+ Thông thường, bài toán quỹ tích ta làm theo các bước:
1, Dự đoán quỹ tích
2, Chứng minh quỹ tích: gồm Phần thuận và Phần đảo
3, Kết luận.
+ Quỹ tích các điểm nhìn đoạn thẳng AB cho trước dưới một góc vuông là đường tròn đường kính AB.
Lời giải
Cách dựng:
+ Dựng đoạn thẳng AB = 3cm.
+ Dựng góc
+ Dựng tia Ay vuông góc với tia Ax.
+ Dựng đường trung trực d của đoạn thẳng AB.
+ d cắt Ay tại O.
+ Dựng đường tròn tâm O, bán kính OA.
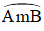
Chứng minh:
+ O thuộc đường trung trực của AB
⇒ OA = OB
⇒ B thuộc đường tròn (O; OA).
Ax ⊥ AO ⇒ Ax là tiếp tuyến của (O; OA).
⇒ 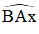
Lấy M ∈ 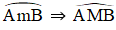
⇒ 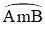
Kết luận: Bài toán có một nghiệm hình.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.