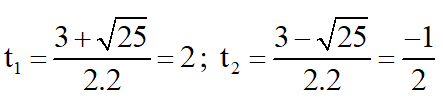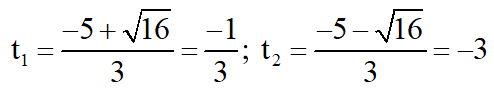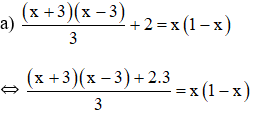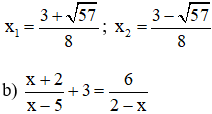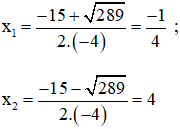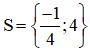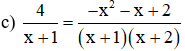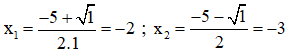Giải bài tập SGK Toán 9 tập 2 hay nhất Bài 7: Phương trình quy về phương trình bậc hai

a) $4x^4+x^2-5=0$

Đặt $x^2=t$(t ≥ 0). Phương trình trở thành:

$4t^2+t-5=0$

Nhận thấy phương trình có dạng a + b + c = 0 nên phương trình có nghiệm

${\text{t}}_1=1;{\text{t}}_2=(-5)/4$

Do t ≥ 0 nên t = 1 thỏa mãn điều kiện

Với t = 1, ta có: $x^2=1\iff x=\pm 1$

Vậy phương trình có 2 nghiệm ${\text{x}}_1=1;{\text{x}}_2=-1$

b) $3x^4+4x^2+1=0$

Đặt $x^2=t(t\ge 0)$. Phương trình trở thành:

$3t^2+4t+1=0$

Nhận thấy phương trình có dạng a - b + c = 0 nên phương trình có nghiệm

$t_1=-1;t_2=(-1)/3$

Cả 2 nghiệm của phương trình đều không thỏa mãn điều kiện t ≥ 0

Vậy phương trình đã cho vô nghiệm.

- Điều kiện: x ≠ ±3

- Khử mẫu và biến đổi, ta được: $$\begin{gathered} x^2 – 3x + 6 = x + 3 \\ \iff x^2 – 4x + 3 = 0. \end{gathered}$$

- Nghiệm của phương trình $x^2 – 4x + 3 = 0 là: x_1 = 1; x_2 = 3$

$x1$ có thỏa mãn điều kiện nói trên

$x2$ không thỏa mãn điều kiện nói trên

Vậy nghiệm của phương trình đã cho là: x = 1

$x^3 + 3x^2 + 2x = 0 \iff x(x^2 + 3x + 2) = 0$

⇔ x = 0 hoặc $x^2 + 3x + 2 = 0 \left(1\right)$

Giải phương trình (1) ta được các nghiệm x = -1; x = -2

Vậy phương trình đã cho có 3 nghiệm x = 0; x = -1; x = -2

a) $x^4 – 5x^2 + 4 = 0 \left(1\right)$

Đặt $x^{\mathit{2}} =$t, điều kiện t ≥ 0.

Khi đó (1) trở thành : $t^2 – 5t + 4 = 0 \left(2\right)$

Giải (2) : Có a = 1 ; b = -5 ; c = 4 ⇒ a + b + c = 0

⇒ Phương trình có hai nghiệm $t_1 = 1; t_2 = c/a = 4$

Cả hai giá trị đều thỏa mãn điều kiện.

+ Với t = 1 ⇒ $x^2 = 1$ ⇒ x = 1 hoặc x = -1;

+ Với t = 4 ⇒ $x^2 = 4$ ⇒ x = 2 hoặc x = -2.

Vậy phương trình (1) có tập nghiệm S = {-2 ; -1 ; 1 ; 2}.

b) $2x^4 – 3x^2 – 2 = 0; \left(1\right)$

Đặt $x^2 = t$, điều kiện t ≥ 0.

Khi đó (1) trở thành : $2t^2 – 3t – 2 = 0 \left(2\right)$

Giải (2) : Có a = 2 ; b = -3 ; c = -2

$\Rightarrow \Delta = {(-3)}^2 - 4.2.(-2) = 25 > 0$

⇒ Phương trình có hai nghiệm

Chỉ có giá trị $t_1 = 2$ thỏa mãn điều kiện.

+ Với t = 2 ⇒ $x^2 = 2$ ⇒ x = √2 hoặc x = -√2;

Vậy phương trình (1) có tập nghiệm S = {-√2 ; √2}.

c) $3x^4 + 10x^2 + 3 = 0 \left(1\right)$

Đặt $x^2 = t$, điều kiện t ≥ 0.

Khi đó (1) trở thành : $3t^2 + 10t + 3 = 0 \left(2\right)$

Giải (2) : Có a = 3; b' = 5; c = 3

⇒ $\Delta ’ = 5^2 – 3.3 = 16 > 0$

⇒ Phương trình có hai nghiệm phân biệt

Cả hai giá trị đều không thỏa mãn điều kiện.

Vậy phương trình (1) vô nghiệm.

⇔ (x + 3)(x – 3) + 2.3 = 3x(1 – x)

$\begin{array}{l}\iff x^2-9+6=3x-3x^2\\ \iff x^2-9+6-3x+3x^2=0\\ \iff 4x^2-3x-3=0\end{array}$

Có a = 4; b = -3; c = -3 $\Rightarrow \Delta = {(-3)}^2 – 4.4.(-3) = 57 > 0$

Phương trình có hai nghiệm

Điều kiện xác định: x ≠ 5; x ≠ 2.

Quy đồng và khử mẫu ta được :

(x + 2)(2 – x) + 3(2 – x)(x – 5) = 6(x – 5)

$\begin{array}{l}\iff 4-x^2+6x-3x^2-30+15x=6x-30\\ \iff 4-x^2+6x-3x^2-30+15x-6x+30=0\\ \iff -4x^2+15x+4=0\end{array}$

Có a = -4; b = 15; c = 4 $\Rightarrow \Delta = {15}^2 – 4.(-4).4 = 289 > 0$

Phương trình có hai nghiệm phân biệt:

Cả hai giá trị đều thỏa mãn điều kiện.

Vậy phương trình có tập nghiệm 

Điều kiện xác định: x ≠ -1; x ≠ -2.

Quy đồng và khử mẫu ta được:

$\begin{array}{l}4\cdot (x+2)=-x^2-x+2\\ \iff 4x+8=-x^2-x+2\\ \iff 4x+8+x^2+x-2=0\\ \iff x^2+5x+6=0\end{array}$

Có a = 1; b = 5; c = 6 $\Rightarrow \Delta = 5^2 – 4.1.6 = 1 > 0$

⇒ Phương trình có hai nghiệm phân biệt:

Chỉ có nghiệm $x_2 = -3$ thỏa mãn điều kiện xác định.

Vậy phương trình có nghiệm x = -3.

a)

$\begin{array}{l}\left(3x^2-5x+1\right)\left(x^2-4\right)=0\\ \iff 3x^2-5x+1=0\end{array}$

hoặc $x^2 – 4 = 0 \left(2\right)$

+ Giải (1): $3x^2 – 5x + 1 = 0$

Có a = 3; b = -5; c = 1 $\Rightarrow \Delta = {(-5)}^2 – 4.3 = 13 > 0$

Phương trình có hai nghiệm: 

+ Giải (2): $x^2 – 4 = 0 \iff x^2 = 4$ ⇔ x = 2 hoặc x = -2.

Vậy phương trình có tập nghiệm 

b) 

$\begin{array}{l}{\left(2x^2+x-4\right)}^2-{(2x-1)}^2=0\\ \iff \left(2x^2+x-4-2x+1\right)\left(2x^2+x-4+2x-1\right)=0\\ \iff \left(2x^2-x-3\right)\left(2x^2+3x-5\right)=0\\ \iff 2x^2-x-3=0\left(1\right)\end{array}$

hoặc $2x^2 + 3x – 5 = 0 \left(2\right)$

+ Giải (1): $2x^2 – x – 3 = 0$

Có a = 2; b = -1; c = -3 ⇒ a – b + c = 0

⇒ Phương trình có hai nghiệm x = -1 và x = -c/a = 3/2.

+ Giải (2): $2x^2 + 3x – 5 = 0$

Có a = 2; b = 3; c = -5 ⇒ a + b + c = 0

⇒ Phương trình có hai nghiệm x = 1 và x = c/a = -5/2.

Vậy phương trình có tập nghiệm