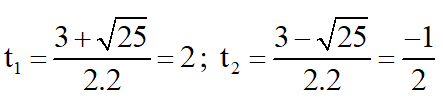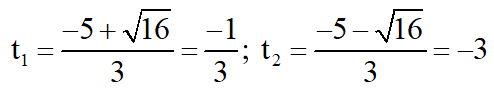Giải phương trình sau bằng cách đưa về phương trình tích: $x^3 + 3x^2+ 2x = 0.$

a) $4x^4+x^2-5=0$

Đặt $x^2=t$(t ≥ 0). Phương trình trở thành:

$4t^2+t-5=0$

Nhận thấy phương trình có dạng a + b + c = 0 nên phương trình có nghiệm

${\text{t}}_1=1;{\text{t}}_2=(-5)/4$

Do t ≥ 0 nên t = 1 thỏa mãn điều kiện

Với t = 1, ta có: $x^2=1\iff x=\pm 1$

Vậy phương trình có 2 nghiệm ${\text{x}}_1=1;{\text{x}}_2=-1$

b) $3x^4+4x^2+1=0$

Đặt $x^2=t(t\ge 0)$. Phương trình trở thành:

$3t^2+4t+1=0$

Nhận thấy phương trình có dạng a - b + c = 0 nên phương trình có nghiệm

$t_1=-1;t_2=(-1)/3$

Cả 2 nghiệm của phương trình đều không thỏa mãn điều kiện t ≥ 0

Vậy phương trình đã cho vô nghiệm.

a) $x^4 – 5x^2 + 4 = 0 \left(1\right)$

Đặt $x^{\mathit{2}} =$t, điều kiện t ≥ 0.

Khi đó (1) trở thành : $t^2 – 5t + 4 = 0 \left(2\right)$

Giải (2) : Có a = 1 ; b = -5 ; c = 4 ⇒ a + b + c = 0

⇒ Phương trình có hai nghiệm $t_1 = 1; t_2 = c/a = 4$

Cả hai giá trị đều thỏa mãn điều kiện.

+ Với t = 1 ⇒ $x^2 = 1$ ⇒ x = 1 hoặc x = -1;

+ Với t = 4 ⇒ $x^2 = 4$ ⇒ x = 2 hoặc x = -2.

Vậy phương trình (1) có tập nghiệm S = {-2 ; -1 ; 1 ; 2}.

b) $2x^4 – 3x^2 – 2 = 0; \left(1\right)$

Đặt $x^2 = t$, điều kiện t ≥ 0.

Khi đó (1) trở thành : $2t^2 – 3t – 2 = 0 \left(2\right)$

Giải (2) : Có a = 2 ; b = -3 ; c = -2

$\Rightarrow \Delta = {(-3)}^2 - 4.2.(-2) = 25 > 0$

⇒ Phương trình có hai nghiệm

Chỉ có giá trị $t_1 = 2$ thỏa mãn điều kiện.

+ Với t = 2 ⇒ $x^2 = 2$ ⇒ x = √2 hoặc x = -√2;

Vậy phương trình (1) có tập nghiệm S = {-√2 ; √2}.

c) $3x^4 + 10x^2 + 3 = 0 \left(1\right)$

Đặt $x^2 = t$, điều kiện t ≥ 0.

Khi đó (1) trở thành : $3t^2 + 10t + 3 = 0 \left(2\right)$

Giải (2) : Có a = 3; b' = 5; c = 3

⇒ $\Delta ’ = 5^2 – 3.3 = 16 > 0$

⇒ Phương trình có hai nghiệm phân biệt

Cả hai giá trị đều không thỏa mãn điều kiện.

Vậy phương trình (1) vô nghiệm.