Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây

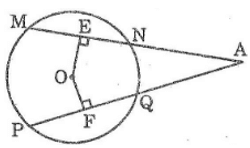
Nối OA

Ta có: MN = PQ (gt)

Suy ra: OE = OF (hai dây bằng nhau cách đều tâm)

Xét hai tam giác OAE và OAF, ta có: 

OA chung

OE = OF (chứng minh trên)

Suy ra: ΔOAE = ΔOAF (cạnh huyền, cạnh góc vuông)

Suy ra: AE = AF

Ta có: OE ⊥ MN (gt)

Suy ra EN = (1/2).MN (đường kính vuông góc với dây cung)     (1)

OF ⊥ PQ (gt)

Suy ra FQ = (1/2).PQ (đường kính vuông góc với dây cung)     (2)

Mặt khác: MN = PQ (gt)     (3)

Từ (1), (2) và (3) suy ra: EN = FQ     (4)

Mà AE = QF (chứng minh trên)     (5)

Từ (4) và (5) suy ra: AN + NE = AQ + QF     (6)

Từ (5) và (6) suy ra: AN = AQ

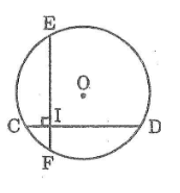
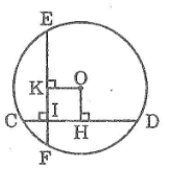
Kẻ OH ⊥ CD, OK ⊥ EF

Vì tứ giác OKIH có ba góc vuông nên nó là hình chữ nhật.

Ta có: CD = EF (gt)

Suy ra: OH = OK (hai dây bằng nhau cách đều tâm)

Suy ra tứ giác OKIH là hình vuông.

Ta có:

CD = CI + ID = 2 + 14 = 16(cm)

HC = HD = CD/2 = 8 (cm) (đường kính dây cung)

IH = HC - CI = 8 - 2 = 6 (cm)

Suy ra: OH = OK = 6 (cm) (OKIH là hình vuông)

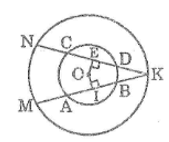
Kẻ OI ⊥ AB, OE ⊥ CD

Trong (O; OA) ta có: AB < CD (gt)

Suy ra : OI > OE (dây lớn hơn gần tâm hơn)

Trong (O ; OK) ta có : OI > OE (cmt)

Suy ra : KM < KN (dây gần tâm hơn thì lớn hơn)

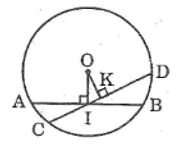
Gọi CD là dây bất kì đi qua I và CD không vuông góc với OI.

Kẻ OK ⊥ CD

Tam giác OKI vuông tại K nên OI > OK

Suy ra : AB < CD (dây lớn hơn gần tâm hơn)

Vậy dây AB vuông góc với IO tại I ngắn hơn mọi dây khác đi qua I.

Tam giác ABC có  nên suy ra :

BC > AC > AB (cạnh đối diện góc lớn hơn thì lớn hơn)

Ta có AB, BC, AC lần lượt là các dây cung của đường tròn (O)

Mà BC > AC > AB nên suy ra:

OH < OI < OK (dây lớn hơn gần tâm hơn)

Kẻ OH ⊥ AB, OK ⊥ CD

Ta có: AB = CD (gt)

Suy ra : OH = OK (hai dây bằng nhau cách đều tâm)

Vậy OI là tia phân giác của góc BID (tính chất đường phân giác)

Xét hai tam giác OIH và OIK, ta có :

OI chung

OH = OK (chứng minh trên)

Suy ra: $∆$OIH = $∆$OIK (cạnh huyền, cạnh góc vuông)

Suy ra: IH = IK     (1)

Lại có: HA = HB = (1/2).AB

KC = KD = (1/2).CD

Mà AB = CD nên HA = KC     (2)

Từ (1) và (2) suy ra: IA = IC

Mà AB = CD nên IB = ID

Kẻ OK ⊥ CD ⇒ CK = DK = (1/2).CD

Kẻ OH ⊥ AB ⇒ AH = BH = (1/2).AB

Vì AB // CD nên H, O, K thẳng hàng

Áp dụng định lí Pitago vào tam giác vuông OBH ta có:

$O{B}^2=B{H}^2+O{H}^2$

Suy ra: $O{H}^2=O{B}^2-B{H}^2={25}^2-{20}^2$= 225

OH = 15 (cm)

Áp dụng định lí Pitago vào tam giác vuông ODK ta có:

$O{D}^2=D{K}^2+O{K}^2$

Suy ra: $O{K}^2=O{D}^2-D{K}^2={25}^2-{24}^2$ = 49

OK = 7 (cm)

* Trường hợp O nằm giữa hai dây AB và CD (hình a):

HK = OH + OK = 15 + 7 = 22 (cm)

* Trường hợp O nằm ngoài hai dây AB và CD (hình b):

HK = OH – OK = 15 – 7 = 8 (cm)

Kẻ OH ⊥ AM, OK ⊥ AN

Ta có: AM = AN (gt)

Suy ra: OH = OK (hai dây bằng nhau cách đều tâm)

Xét hai tam giác OCH và OCK, ta có:

OC chung

OH = OK (chứng minh trên)

Suy ra: $∆$OIH = $∆$OIK (cạnh huyền, cạnh góc vuông)

Xét hai tam giác OAH và OBH, ta có:

OA = OB

OH = OK (chứng minh trên)

Suy ra: $∆$OAH = $∆$OBH (cạnh huyền, cạnh góc vuông)

Tam giác OAB cân tại O có OC là tia phân giác nên OC đồng thời cũng là đường cao (tính chất tam giác cân)

Suy ra: OC ⊥ AB

Dây đi qua M ngắn nhất là dây AB vuông góc với OM

Áp dụng định lí Pitago vào tam giác vuông OAM ta có:

$O{A}^2=A{M}^2+O{M}^2$

Suy ra: $A{M}^2=O{A}^2-O{M}^2=5^2-3^2$= 16

AM = 4 (dm)

Ta có: OM ⊥ AB

Suy ra: AM = (1/2).AB

Hay: AB = 2AM = 2.4 = 8 (dm)

Dây đi qua M lớn nhất khi nó là đường kính của đường tròn (O). Vậy dây có độ dài bằng 2R = 2.5 = 10 (dm)

Ta có: HA = HB (gt)

Suy ra : OH ⊥ AB (đường kính dây cung)

Lại có : KC = KD (gt)

Suy ra : OK ⊥ CD (đường kính dây cung)

Mà AB > CD (gt)

Nên OK > OH (dây lớn hơn gần tâm hơn)

Áp dụng định lí Pitago vào tam giác vuông OHM ta có :

$O{M}^2=O{H}^2+H{M}^2$

Suy ra : $H{M}^2=O{M}^2-O{H}^2$ (1)

Áp dụng định lí Pitago vào tam giác vuông OKM ta có:

$O{M}^2=O{K}^2+K{M}^2$

Suy ra: $K{M}^2=O{M}^2-O{K}^2$ (2)

Mà OH < OK (cmt) (3)

Từ (1), (2) và (3) suy ra: $H{M}^2>K{M}^2$ hay HM > KM

* Cách dựng

- Dựng trung điểm I của AB

- Qua A dựng dây CD song song với OI

- Qua B dựng dây EF song song với OI

Ta được CD và EF là hai dây cần dựng

* Chứng minh

Ta có : CD // OI, EF // OI

Suy ra : CD // EF

Kẻ OH ⊥ CD cắt EF tại K

Suy ra: OK ⊥ EF

Lại có: IA = IB

Suy ra: OH = OK

Vậy CD = EF.

Chọn đáp án D

Dây AB phải dựng vuông góc với OI tại I.

Dây lớn nhất đi qua C là đường kính EF = 50cm. Dây nhỏ nhất đi qua C là dây AB vuông góc với OC tại C, AB = 48 cm.

Có tất cả 4 dây đi qua C có độ dài là một số nguyên xentimet.