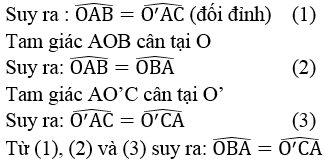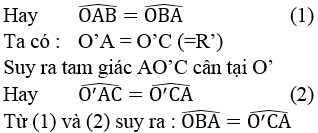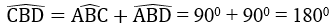Bài 7: Vị trí tương đối của hai đường tròn
43 người thi tuần này 4.6 64.3 K lượt thi 11 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
20 bài tập Toán 9 Cánh diều Bài 2. Hình nón có đáp án
Danh sách câu hỏi:
Lời giải
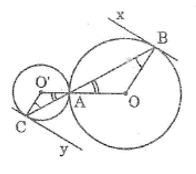
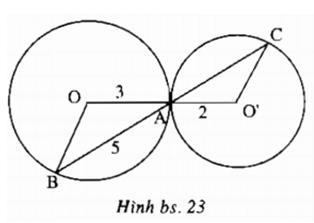
Ta có: O, A, O’ thẳng hàng
C, A, B thẳng hàng
Lời giải
Gọi H là giao điểm của AB và OO’.
Vì OO’ là đường trung trực của AB nên:
OO’ ⊥ AB tại H
Suy ra: HA = HB = (1/2).AB = (1/2).24 = 12 (cm)
Áp dụng định lí Pitago vào tam giác vuông AOH, ta có:
Suy ra: = 81
OH = 9 (cm)
Áp dụng định lí pitago vào tam giác vuông AO’H, ta có:
Suy ra: = 25
O’H = 5 (cm)
Vậy OO’ = OH + O’H = 9 + 5 = 14 (cm)
Lời giải
Ta có: OA = OB (= R)
Suy ra tam giác AOB cân tại O
Suy ra: OB // O’C (vì có hai góc ở vị trí đồng vị bằng nhau)
Lời giải
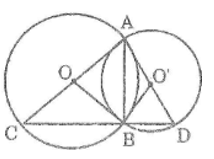
Tam giác ABC nội tiếp trong đường tròn (O) có AC là đường kính nên góc (ABC) =
Tam giác ABD nội tiếp trong đường tròn (O’) có AD là đường kính nên góc (ABD) =
Ta có:
Vậy ba điểm C, B, D thẳng hàng và AB ⊥ CD
Lời giải
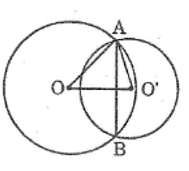
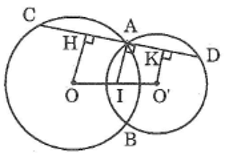
Kẻ OH ⊥ CD, O’K ⊥ CD
Ta có: IA ⊥ CD
Suy ra : OH // IA // O’K
Theo giả thiết : IO = IO’
Suy ra : AH = AK (tính chất đường thẳng song song cách đều) (1)
Ta có : OH ⊥ AC
Suy ra : HA = HC = (1/2).AC (đường kính dây cung) ⇒ AC = 2AH (2)
Lại có : O’K ⊥ AD
Suy ra : KA = KD = (1/2).AD (đường kính dây cung) ⇒ AD = 2AK (3)
Từ (1), (2) và (3) suy ra: AC = AD
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.