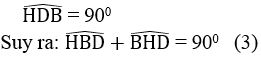Bài 5: Dấu hiệu nhận biết tiếp tuyến của đường tròn.

* Phân tích

Giả sử tiếp tuyến AB và AC cần dựng thỏa mãn điều kiện bài toán

Ta có: AB ⊥ OB ⇒ $\angle$ABO = $90°$

AC ⊥ OC ⇒ $\angle$ACO = $90°$

Tam giác ABO có $\angle$ABO = $90°$ nội tiếp trong đường tròn đường kính AO và tam giác ACO có $\angle$ACO = 90o nội tiếp trong đường tròn đường kính AO.

Suy ra B và C là giao điểm của đường tròn đường kính AO với đường tròn (O).

* Cách dựng

- Dựng I là trung điểm của OA

- Dựng đường tròn (I; IO) cắt đường tròn (O) tại B và C

- Nối AB, AC ta được hai tiếp tuyến cần dựng

* Chứng minh

Tam giác ABO nội tiếp trong đường tròn (I) có OA là đường kính nên: $\angle$ABO = $90°$

Suy ra: AB ⊥ OB tại B nên AB là tiếp tuyến của đường tròn (O)

Tam giác ACO nội tiếp trong đường tròn (I) có OA là đường kính nên: $\angle$ACO = $90°$

Suy ra: AC ⊥ OC tại C nên AC là tiếp tuyến của đường tròn (O)

* Biện luận

Luôn dựng được đường tròn tâm I, cắt đường tròn tâm O tại hai điểm B và C và luôn có AB, AC là hai tiếp tuyến của đường tròn (O).

* Phân tích

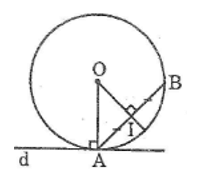
- Giả sử dựng được đường tròn (O) qua A, B và tiếp xúc với d. Khi đó đường tròn (O) phải tiếp xúc với d tại A

- Đường tròn (O) đi qua A và B nên tâm O nằm trên đường trung trực của AB

- Đường tròn (O) tiếp xúc với d tại A nên điểm O nằm trên đường thẳng vuông góc với d tại điểm A

* Cách dựng

- Dựng đường thẳng trung trực của AB

- Dựng đường thẳng đi qua A và vuông góc với d. Đường thẳng này cắt đường trung trực của AB tại O

- Dựng đường tròn (O; OA) ta được đường tròn cần dựng

* Chứng minh

Vì O nằm trên đường trung trực của AB nên OA = OB. Khi đó đường tròn (O; OA) đi qua hai điểm A và B

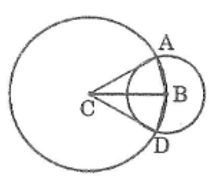
Xét hai tam giác ABC và DBC, ta có:

BA = BD (bán kính của (B; BA))

CA = CD (bán kính của (C; CA))

BC chung

Suy ra: $∆$ABC = $∆$DBC (c.c.c)

Suy ra: CD ⊥ BD tại D

Vậy CD là tiếp tuyến của đường tròn (B; BA)

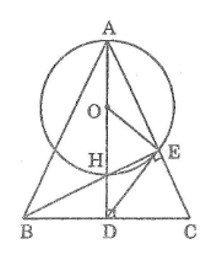
Gọi O là trung điểm của AH

Tam giác AEH vuông tại E có EO là đường trung tuyến nên :

EO = OA = OH = AH/2 (tính chất tam giác vuông)

Vậy điểm E nằm trên đường tròn (O ; AH/2 )

Ta có : OH = OE

Suy ra tam giác OHE cân tại O

Trong tam giác BDH ta có:

Từ (1), (2) và (3) suy ra:

Tam giác ABC cân tại A có AD ⊥ BC nên BD = CD

Tam giác BCE vuông tại E có ED là đường trung tuyến nên:

ED = DB = BC/2 (tính chất tam giác vuông)

Suy ra tam giác BDE cân tại D

Suy ra: DE ⊥ EO. Vậy DE là tiếp tuyến của đường tròn (O).