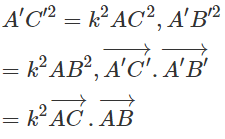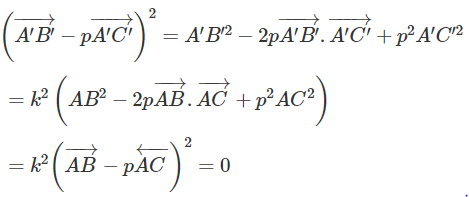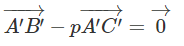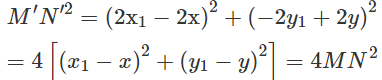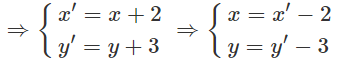Gọi A’, B’ và C’ tương ứng là ảnh của ba điểm A, B và C qua phép đồng dạng. Chứng minh rằng nếu , trong đó p là một số. Từ đó chứng minh rằng phép đồng dạng biến ba điểm thẳng hàng thành ba điểm thẳng hàng và nếu điểm B nằm giữa hai điểm A và C thì điểm B' nằm giữa hai điểm A’ và C’.
Câu hỏi trong đề: Giải sách bài tập Hình học 11 !!
Quảng cáo
Trả lời:
Để ý rằng
Ta có:
Từ đó suy ra
Giả sử ba điểm A, B, C thẳng hàng và điểm B nằm giữa hai điểm A và C. Khi đó , với 0 < t < 1. Áp dụng bài 1.39 ta cũng có , với 0 < t < 1. Do đó ba điểm A′, B′, C′ thẳng hàng và điểm B' nằm giữa hai điểm A' và C'.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lấy điểm , thì điểm . Ta có
Từ đó suy ra với hai điểm M, N tùy ý và M', N' lần lượt là ảnh của chúng qua F ta có M′N′ = 2MN. Vậy F là phép đồng dạng với tỉ số đồng dạng là 2.
Lời giải
Gọi M′(x′;y′) ∈ d′ là ảnh của M(x,y) ∈ d qua phép tịnh tiến theo vecto
Do M(x,y) ∈ d nên
3x − 5y + 3 = 0
⇒ 3(x′−2) − 5(y′−3) + 3 = 0
⇔ 3x′ − 5y′ + 12 = 0 (d′)
Vậy M′(x′;y′) ∈ d′: 3x′ − 5y′ + 12 = 0
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.