Câu hỏi:

24/06/2020 505

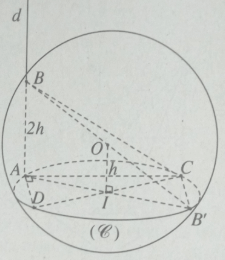
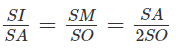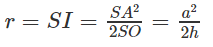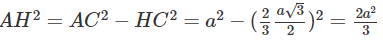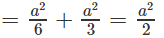Cho mặt cầu tâm O bán kính r. Gọi ( $α$ ) là mặt phẳng cách tâm O một khoảng h (0 < h < r) và cắt mặt cầu theo đường tròn (C). Đường thẳng d đi qua một điểm A cố định trên (C) và vuông góc với mặt phẳng ( $α$ ) cắt mặt cầu tại một điểm B. Gọi CD là đường kính di động của (C). Tìm tập hợp các điểm H, hình chiếu của B trên CD khi CD chuyển động trên đường tròn (C).

Xem lời giải

Câu hỏi trong đề: Giải SBT Toán 12 Bài 2: Mặt cầu !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Giải sách bài tập Toán 12 | Giải sbt Toán 12

Ta có AH $⊥$ DC. Do đó khi CD di động, điểm H luôn luôn nhìn đọan thẳng AI dưới một góc vuông. Vậy tập hợp các điểm H là đường tròn đường kính AI nằm trong mặt phẳng ( $α$ ).

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Hình chóp tam giác S.ABC có SA = SB = SC = a và có chiều cao bằng h. Xác định tâm và bán kính của mặt cầu ngoại tiếp hình chóp. Tính diện tích của mặt cầu đó.

Xem đáp án

Lời giải

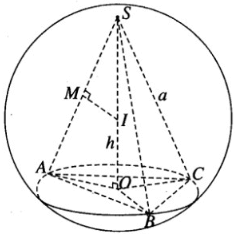
Giải sách bài tập Toán 12 | Giải sbt Toán 12

Giả sử ta có mặt cầu tâm I đi qua các đỉnh S, A, B, C của hình chóp. Mặt phẳng (ABC) cắt mặt cầu ngoại tiếp hình chóp theo giao tuyến là đường tròn tâm O ngoại tiếp tam giác ABC. Vì SA = SB = SC nên ta có SO $⊥$ (ABC) và OS là trục của đường tròn tâm O. Do đó SO $⊥$ AO. Trong tam giác SAO, đường trung trực của đoạn SA cắt SO tại I và ta được hai tam giác vuông đồng dạng là SIM và SAO, với M là trung điểm của cạnh SA.

Ta có Giải sách bài tập Toán 12 | Giải sbt Toán 12

với SI = IA = IB = IC = r

Vậy Giải sách bài tập Toán 12 | Giải sbt Toán 12

Do đó diện tích của mặt cầu ngoại tiếp hình chóp S.ABC đã cho là :

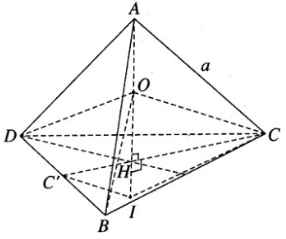
Giải sách bài tập Toán 12 | Giải sbt Toán 12

Câu 2

Hình tứ diện đều ABCD có cạnh bằng a và có đường cao AH. Gọi O là trung điểm của AH. Xác định tâm và bán kính của mặt cầu ngoại tiếp tứ diện OBCD.

Xem đáp án

Lời giải

Giải sách bài tập Toán 12 | Giải sbt Toán 12

Gọi H trọng tâm của tam giác đều BCD.

Ta có AH $⊥$ (BCD). Do đó

Giải sách bài tập Toán 12 | Giải sbt Toán 12

Vậy

Giải sách bài tập Toán 12 | Giải sbt Toán 12

Mặt khác ${OC}^{2} = {OH}^{2} + {HC}^{2}$

Giải sách bài tập Toán 12 | Giải sbt Toán 12

hay OC = OB = OD = (a $\sqrt{2}$ )/2

Vì BD = BC = CD = a nên các tam giác DOB, BOC, COD là những tam giác vuông cân tại O. Do đó hình chóp ODBC là hình chóp có đáy là tam giác đều nên tâm của mặt cầu ngoại tiếp phải nằm trên OH, ngoài ra tâm của mặt cầu ngoại tiếp này phải nằm trên trục của tam giác vuông DOB. Từ trung điểm C’ của cạnh BD ta vẽ đường thẳng song song với OC cắt đường thẳng OH tại I. Ta có I là tâm mặt cầu ngoại tiếp tứ diện OBCD. Mặt cầu này có bán kính là IC và ${IC}^{2} = {IH}^{2} + {HC}^{2}$

Chú ý rằng IH = OH/2 (vì HC′ = HC/2)

Do đó:

Câu 3

Hình chóp S.ABCD có SA = a là chiều cao của hình chóp và đáy ABCD là hình thang vuông tại A và B có AB = BC = a và AD = 2a. Gọi E là trung điểm của cạnh AD. Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp S.CDE

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho hình cầu đường kính AA’ = 2r. Gọi H là một điểm trên đoạn AA’ sao cho AH = 4r/3. Mặt phẳng ( $α$ ) qua H và vuông góc với AA’ cắt hình cầu theo đường tròn (C). Tính diện tích của hình tròn (C) .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho tứ diện SABC có cạnh SA vuông góc với mặt phẳng (ABC) và có SA = a, AB = b , AC = c . Xác định tâm và bán kính hình cầu ngoại tiếp tứ diện trong các trường hợp sau: $∠$ BAC = 90 $°$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Chứng minh rằng nếu có một mặt cầu tiếp xúc với 6 cạnh của một hình tứ diện thì hình tứ diện đó có tổng các cặp cạnh đối diện bằng nhau.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Cho tứ diện SABC có cạnh SA vuông góc với mặt phẳng (ABC) và có SA = a, AB = b , AC = c . Xác định tâm và bán kính hình cầu ngoại tiếp tứ diện trong các trường hợp sau: $∠$ BAC = 120 $°$ và b = c

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Bình luận

Hình chóp tam giác S.ABC có SA = SB = SC = a và có chiều cao bằng h. Xác định tâm và bán kính của mặt cầu ngoại tiếp hình chóp. Tính diện tích của mặt cầu đó.

Hình tứ diện đều ABCD có cạnh bằng a và có đường cao AH. Gọi O là trung điểm của AH. Xác định tâm và bán kính của mặt cầu ngoại tiếp tứ diện OBCD.

Hình chóp S.ABCD có SA = a là chiều cao của hình chóp và đáy ABCD là hình thang vuông tại A và B có AB = BC = a và AD = 2a. Gọi E là trung điểm của cạnh AD. Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp S.CDE

Cho hình cầu đường kính AA’ = 2r. Gọi H là một điểm trên đoạn AA’ sao cho AH = 4r/3. Mặt phẳng (α) qua H và vuông góc với AA’ cắt hình cầu theo đường tròn (C). Tính diện tích của hình tròn (C) .

Cho tứ diện SABC có cạnh SA vuông góc với mặt phẳng (ABC) và có SA = a, AB = b , AC = c . Xác định tâm và bán kính hình cầu ngoại tiếp tứ diện trong các trường hợp sau: ∠BAC = 90°

Chứng minh rằng nếu có một mặt cầu tiếp xúc với 6 cạnh của một hình tứ diện thì hình tứ diện đó có tổng các cặp cạnh đối diện bằng nhau.

Cho tứ diện SABC có cạnh SA vuông góc với mặt phẳng (ABC) và có SA = a, AB = b , AC = c . Xác định tâm và bán kính hình cầu ngoại tiếp tứ diện trong các trường hợp sau: ∠BAC = 120° và b = c

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho hình cầu đường kính AA’ = 2r. Gọi H là một điểm trên đoạn AA’ sao cho AH = 4r/3. Mặt phẳng ( $α$ ) qua H và vuông góc với AA’ cắt hình cầu theo đường tròn (C). Tính diện tích của hình tròn (C) .

Cho tứ diện SABC có cạnh SA vuông góc với mặt phẳng (ABC) và có SA = a, AB = b , AC = c . Xác định tâm và bán kính hình cầu ngoại tiếp tứ diện trong các trường hợp sau: $∠$ BAC = 90 $°$

Cho tứ diện SABC có cạnh SA vuông góc với mặt phẳng (ABC) và có SA = a, AB = b , AC = c . Xác định tâm và bán kính hình cầu ngoại tiếp tứ diện trong các trường hợp sau: $∠$ BAC = 120 $°$ và b = c