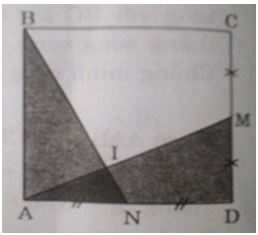
Cho hình vuông ABCD, M là trung điểm của CD, N là trung điểm của AD. Gọi I là giao điểm của AM và BN.
Chứng minh rằng:
Quảng cáo
Trả lời:
Giải bởi Vietjack
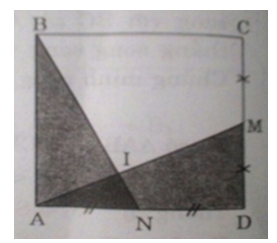
Xét ΔBAN và ΔADM có:
AB = AD (ABCD là hình vuông)
(BAN) = (ADM) = 90o
AN = MD (= 1/2 cạnh hình vuông)
⇒ ΔBAN = ΔADM (c.g.c)
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
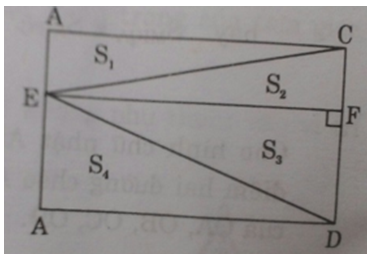
Kẻ EF ⊥ CD ⇒ AC // EF // AD
Xét ΔBCE và ΔFEC có:
(CAE) = (CFE) = 90o
(BCE) = (CEF) (Hai góc so le trong)
CE chung
⇒ ΔBCE = ΔFEC (cạnh huyền- góc nhọn)
tương tự ΔAED=ΔFDE.
Do đó (theo hình vẽ):
S1 = S2 và S3 = S4
⇒ S2 + S3 = S1 + S4 = (1/2)SABCD
Hay SECD = (1/2)SABCD ⇒ SABCD = 2SECD.
Nhắn tin Zalo
Hỏi bài tập