Câu hỏi:
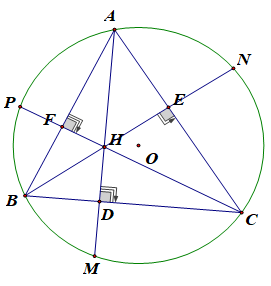
11/07/2024 3,794Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M, N, P. Chứng minh rằng:
b) Bốn điểm B, C, E, F cùng nằm trên một đường tròn
Câu hỏi trong đề: Đề kiểm tra 1 tiết Toán 9 Chương 3 Hình học có đáp án !!
Bắt đầu thiQuảng cáo
Trả lời:
Giải bởi Vietjack
b) Xét tứ giác BFEC có:
∠(BFC) = (Do CF là đường cao)
∠(BEC ) = (Do BE là đường cao)
⇒ E và F cùng nhìn BC dưới một góc bằng nhau
⇒ Tứ giác BFEC nội tiếp được đường tròn
⇒ Bốn điểm B, E, F, C cùng nằm trên đường tròn
Nhà sách vietjack
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Biết diện tích hình tròn là 64π () . Chu vi hình tròn này bằng:
Xem đáp án »
04/07/2020
8,210
Câu 2:
Phần tự luận
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M, N, P. Chứng minh rằng:
a) Tứ giác CEHD nội tiếp
Xem đáp án »
11/07/2024
5,432
Câu 3:
Cho đường tròn O và góc nội tiếp ∠BAC = . Số đo độ của cung nhỏ BC bằng:
Xem đáp án »
04/07/2020
4,035
Câu 4:
Cho tam giác ABC nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H. Các tứ giác nào sau đây nội tiếp được đường tròn.
Xem đáp án »
04/07/2020
2,042
Câu 5:
Cho tứ giác ABCD nội tiếp đường tròn (O). Hai cạnh đối AB và CD cắt nhau tại một điểm M ở ngoài (O), biết ∠BAD = thì góc BMC bằng:
Xem đáp án »
04/07/2020
2,022
Câu 6:
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M, N, P. Chứng minh rằng:
d) H và M đối xứng nhau qua BC
Xem đáp án »
11/07/2024
1,987
🔥 Đề thi HOT:
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
Bộ 5 đề thi giữa kì 2 Toán 9 Kết nối tri thức có đáp án - Đề 01
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 9 Chân trời sáng tạo có đáp án (Đề số 1)
-
Bộ 5 đề thi giữa kì 2 Toán 9 Kết nối tri thức có đáp án - Đề 03
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận