Phần tự luận (7 điểm)
Cho hình hộp chữ nhật MNPQ.EFGH
a) Tìm giao tuyến của hai mặt phẳng (MNFE) và (QNFH).
b) Chứng minh: QH ⊥ mp(EFGH)
Quảng cáo
Trả lời:
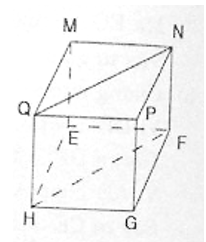
a) Ta có:
NF ⊂ mp(MNEF)
NF ⊂ mp(QNFH)
=> NF là giao uyến của hai mặt phẳng (MNFE) và (QNFH)
b) Ta có: QH ⊥ HE (do QHEM là hình chữ nhật)
QH ⊥ HG (do QHGP là hình chữ nhật)
Mà HE ∩ HG = {H}. Suy ra QH ⊥ mp(EFGH)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 5 mặt bên, 5 đỉnh, 5 cạnh bên
B. 5 mặt bên, 10 đỉnh, 10 cạnh bên
C. 5 mặt bên, 10 đỉnh, 5 cạnh bên
D. 7 mặt bên, 10 đỉnh, 7 cạnh bên.
Lời giải
Chọn C
Lời giải

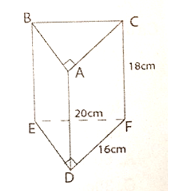
a) Ta có
OC2 = SC2 - SO2 (Pytago)
= 52 - 42 = 9(cm)
=> OC = 3(cm)
=> AC = 6(cm)
AB2 + BC2 = AC2 (pytago)
2BC2 = AC2 (do AB = BC)
BC2 = AC2/2 = 36/2 = 18(cm)
BC = √18 = 3√2 (cm)
Gọi K là trung điểm của BC. Tam giác SBC cân tại S có SH là đường trung tuyến nên SH cũng là đường cao. Suy ra SH ⊥ BC
Do đó

![]()
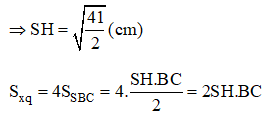

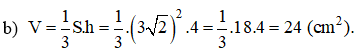
Câu 3
A. 2880
B. 5760
C. 1440
D. 1728
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Hình thoi
B. Hình bình hành
C. Hình chữ nhật
D. Hình thang vuông
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. BC // mp(AA’B’B)
B. BC // mp(A’B’C’D’)
C. BC // mp(ABCD)
D. BC // mp(DCC’D’)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Giao điểm hai đường cao của tam giác ở đáy
B. Giao điểm hai đường trung trực của tam giác ở đáy
C. Giao điểm hai đường trung tuyến của tam giác ở đáy
D. Giao điểm hai đường phân giác ngoài của tam giác ở đáy.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.