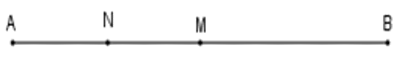Cho n điểm phân biệt (n ≥ 2; n ∈ N) trong đó không có ba điểm nào thẳng hàng. Vẽ các đoạn thẳng nối hai trong n điểm đó. Có tất cả 28 đoạn thẳng. Hãy tìm n.
A. n = 9
B. n = 7
C. n = 8
D. n = 6
Quảng cáo
Trả lời:
Đáp án là C
Số đoạn thẳng tạo thành từ n điểm phân biệt trong đó không có ba điểm nào thẳng hàng là: n(n - 1)/2 (n ≥ 2; n ∈ N)
Theo đề bài có 28 đoạn thẳng được tạo thành nên ta có: n(n - 1)/2 = 28 ⇒ n(n - 1) = 56 = 8.7
Nhận thấy (n - 1) và n là hai số tự nhiên liên tiếp, suy ra n = 8.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 4950 đường thẳng
B. 4590 đường thẳng
C. 9900 đường thẳng
D. 100 đường thẳng
Lời giải
Đáp án là A
Gọi các điểm đó có tên lần lượt là A1, ..., A100
• Qua điểm A1 và 99 điểm còn lại ta vẽ được 99 đường thẳng.
• Qua điểm A2 và 99 điểm còn lại ta vẽ được 99 đường thẳng.
• …
• Qua điểm A100 và 99 điểm còn lại ta vẽ được 99 đường thẳng.
Do đó có 100.99 = 9900 đường thẳng.
Tuy nhiên mỗi đường thẳng lại được tính hai lần nên số đường thẳng được tạo thành là: 9900:2 = 4950 (đường thẳng)
Câu 2
A. 1,5cm
B. 3cm
C. 4,5cm
D. 6cm
Lời giải
Đáp án là D
Vì N là trung điểm đoạn AM nên AN = (1/2)AM hay AM = 2AN = 2.1,5 = 3cm
Lại có điểm M là trung điểm đoạn AB nên ta có AM = (1/2)AB hay AB = 2AM = 2.3 = 6cm
Vậy AB = 6cm
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
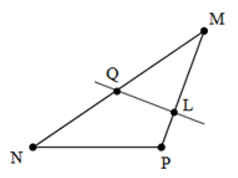
A. MN; MQ; NQ; ML; LP; MP; NP; QL
B. MN; MQ; NQ; ML; LP; MP
C. MN; MQ; NQ; ML; MP; NP
D. MN; MQ; ML; LP; MP; NP
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Song song
B. Trùng nhau
C. Cắt nhau
D. Cả ba đáp án trên đều đúng
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.