Câu hỏi:
13/07/2024 21,191Một số có 2 chữ số . Biết rằng chữ số hàng đơn vị gấp 3 lần chữ số hàng chục. Nếu đổi chỗ 2 chữ số cho nhau được số mới lớn hơn số cũ 54 đơn vị. Tìm số ban đầu
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi số cần tìm là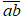 
= 10a + b (a, b ∈ N. 0 < a < b < 10)
Ta có b = 3a
Khi đổi hai chữ số ta được số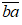 
= 10b + a
Vì số mới lớn hơn số cũ 54 đơn vị nên ta có phương trình: 10b + a – 54 = 10a + b
⇔ 9b – 9a = 54
⇔ 9.3a – 9a = 54
⇔ 18a = 54
⇔ a =3 (tmđk)
Vậy số ban đầu cần tìm là 39.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi số cần tìm là 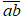= 10a +b (a, b ∈ N; 0 < a < b < 10) .
Ta có a + b = 12 hay b = 12 - a
Khi đổi chỗ hai chữ số thì ta được số mới là 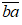= 10b + a
Số mới lớn hơn số cũ 36 đơn vị nên ta có phương trình 10a + b + 36 = 10b + a
Giải phương trình:
10a + b + 36 = 10b + a
⇔ 9a + 36 = 9b
⇔ a + 4 = b
⇔ a + 4 = 12 – a
⇔ 2a = 8
⇔ a = 4 ⇒ b = 8 (tmđk)
Vậy số cần tìm là 48.
Lời giải
Gọi số tự nhiên có hai chữ số cần tìm là 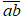= 10a + b (a, b ∈ N,0 < a ≤ 7, 0 ≤ b < 7)
Ta có a + b = 7 .
Khi thêm chữ số 0 vào giữa ta được số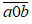 
= 100a + b
Vì số mới hơn số đã cho 180 nên ta có phương trình:
100a + b = 10a + b + 180
⇔ 90a = 180
⇔ a = 2 (tmđk)
⇒ b = 7- a = 5
Vậy số tự nhiên có hai chữ số cần tìm là 25.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 24
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề cuối kì 2 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 1
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận