Câu hỏi:
13/07/2024 2,141Học sinh lớp 6A nhận được phần thưởng từ Liên đội nhà trường, mỗi học sinh đều được nhận số phần thưởng như nhau. Cô tổng phụ trách đã phát hết 215 quyển vở và 129 quyển truyện cho học sinh lớp 6A. Số học sinh của lớp 6A là bao nhiêu, biết rằng số học sinh của lớp nhiều hơn 10 học sinh?
Câu hỏi trong đề: Giải SBT Toán 6 Chương 1: Số tự nhiên - Bộ Cánh diều !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Vì mỗi học sinh đều nhận được phần thưởng là như nhau nên số học sinh vừa là ước của 215 vừa là ước của 129.
Ta có: 215 = 5.43; 129 = 3.43.
Do đó 43 vừa là ước của 215 vừa là ước của 129 và thỏa mãn lớn hơn 10 nên số học sinh của lớp 6A là 43 học sinh.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Ta có: 3n + 13 = 3n + 3 + 10 = 3.(n + 1) + 10.
Vì 3.(n + 1) chia hết cho n + 1 nên để 3n + 13 chia hết cho n + 1 thì 10 phải chia hết cho n + 1 hay n + 1 là ước của 10.
Ta có: 10 = 2.5 nên các ước của 10 là: Ư(10) = {1; 2; 5; 10}.
Ta có bảng sau:
n + 1 | 1 | 2 | 5 | 10 |
n | 0 | 1 | 4 | 9 |
Vậy n ∈ {0; 1; 4; 9}.
b) 5n + 19 chia hết cho 2n + 1.
Vì 5n + 19 chia hết cho 2n + 1 nên 2(5n + 19) chia hết cho 2n + 1
Xét 2(5n + 19) = 10n + 38 = 10n + 5 + 33 = 5(2n + 1) + 33.
Vì 5.(2n + 1) chia hết cho 2n + 1 nên để 2(5n + 19) chia hết cho 2n + 1 thì 33 phải chia hết cho 2n + 1 hay 2n + 1 thuộc ước của 33.
Ta có bảng sau:
2n + 1 | 1 | 3 | 11 | 33 |
n | 0 | 1 | 5 | 16 |
Vậy n ∈ {0; 1; 5; 16}.
Lời giải
a) Số số hạng của VT là: (2n – 2):2 + 1 = n – 1 + 1 = n số.
Khi đó: 2 + 4 + 6 + … + 2.(n – 1) + 2n = (2n + 2).n:2 = n.(n+1).
Theo đầu bài, ta có: n(n + 1) = 210
Ta có:
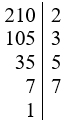
Suy ra 210 = 2.3.4.5= 14.15.
Vậy n = 14.
b) Số số hạng của VT là: (2n – 1 – 1):2 + 1 = (2n – 2):2 + 1 = n – 1 + 1 = n.
Khi đó 1 + 3 + 5 + … + (2n – 3) + (2n – 1) = (2n – 1 + 1).n:2 = 2n.n:2 = n2.
Ta có 223 = 32.52 = 152.
Vậy n = 15.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi Cuối học kì 2 Toán 6 có đáp án (Đề 1)
-
31 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 1: Tập hợp có đáp án
-
Dạng 4: Một số bài tập nâng cao về lũy thừa
-
Đề kiểm tra Giữa kì 2 Toán 6 có đáp án (Mới nhất) - Đề 1
-
10 câu Trắc nghiệm Toán 6 Chân trời sáng tạo Bài 1: Tập hợp. Phần tử của tập hợp (có đáp án)
-
Dạng 4: Trung điểm của đoạn thẳng có đáp án
-
Dạng 6: Bài tập vận dụng có đáp án
-
Đề kiểm tra Giữa kì 2 Toán 6 có đáp án (Mới nhất) - Đề 11